Курсы подготовки МФТИ для школьников
Начало занятий с 8 сентября 2025 года
Подготовительные курсы для школьников – это отличное решение для тех, кто хочет улучшить успеваемость, подготовиться к ЕГЭ, поступлению, к конкурсам или олимпиадам. Выбрав Подготовительные курсы МФТИ, вы можете быть уверены в высоком качестве образовательных услуг, заказать которые можно на выгодных условиях.
Ни для кого не секрет, что подготовка к Единым государственным экзаменам, олимпиадам и поступлению в ВУЗы вызывает массу переживаний у учащихся. Для того, что быть уверенным в собственных силах и знаниях, важно провести тщательную подготовку, восполнить имеющиеся пробелы и укрепить базу знаний.
Подготовительные курсы от МФТИ проходят по программам, утверждённым Учёным советом института. Посещая их, можно не только получить качественную и эффективную подготовку по различным дисциплинам, теоретическую базу и практические навыки, но и избавиться от страха и стать увереннее. Вашему вниманию представлены курсы для выпускников школ, младших школьников и старшеклассников, проводят которые ведущие специалисты с большим опытом.
Программы курсов
![]()
Математика
Олимпиадная математика
Геометрия
Физика
Экспериментальная физика (с октября по апрель)
Олимпиадная физика
Компьютерная физика
Русский язык
Информатика
Программирование
Программирование 7 класс, базовый уровень. Преподаватель курса Лантратов Артем Андреевич Образование КГУ, Краснодар.
Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование. Знакомство с Python. Ввод и вывод данных с помощью функций input() и print(). Переменные и типы данных. Операции с числами. Знакомство с Python. Операции сравнения. Логические операции. Условная конструкция if. Строки. Операции со строками. Методы форматирования строк. Циклы. Работа с циклами while и for. Функция range(). Модуль random. Структуры данных. Списки, словари и множества. Модуль Turtle. Наглядное применение полученных знаний с помощью рисования геометрических фигур. Модуль Turtle. Работа со сложными геометрическими фигурами. Функциональное программирование. Введение в функции. Функции с определённым и неопределённым количеством параметров. Область видимости переменных. Игровое программирование. Создание игры камень, ножницы, бумага. Создание игры кубики яцзы. Игровое программирование. Создание игры Smiley Pong. Игровое программирование. Создание программы Шифр Цезаря. Создание игры крестики-нолики. Игровое программирование. Создание игры “Охотник за сокровищами”. Работа с файлами. Функции read(), readln(), write(), writeln(). Контекстный менеджер with. Создание графического интерфейса. Работа с виджетами и их положением относительно осей x и y. Создание программ с графическим интерфейсом. Создание приложения “Генератор случайных паролей”. Создание программ с графическим интерфейсом. Работа с данными, которые будут нам отдавать другие приложения (API). Создание приложения “Погода”. Создание программ с графическим интерфейсом. Создание приложения “Калькулятор”. Работа с сеткой приложения. Объектно-ориентированное программирование. Классы и объекты. Объектно-ориентированное программирование. Классы и объекты. Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Инкапсуляция”. Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Наследование”. Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Полиморфизм”. Объектно-ориентированное программирование. Изучение класса object. Строковое представление объекта. Объектно-ориентированное программирование. Создание приложения для регистрации пользователя. Приложение будет уметь: Объектно-ориентированное программирование. Создание игры “Властелин разума”. Парсинг данных. BeautifulSoup. Сбор простых данных с сайтов. Парсинг данных. BeautifulSoup. Сбор табличных данных с сайтов. Парсинг данных. BeautifulSoup. Сбор данных с многостраничных сайтов. Парсинг данных. BeautifulSoup. Применение продвинутых техник при сборе данных. Парсинг данных. BeautifulSoup. Сбор данных с сайтов с подгружаемой информацией (данные подгружаются с помощью JavaScript). Парсинг данных. Selenium. Сбор данных с помощью эмуляции работы пользователя. Парсинг данных. Selenium + BeautifulSoup. Комбинируем две библиотеки для оптимизации процесса сбора данных. Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование. Курс рассчитан на более глубокое погружение в сам язык программирования. Будем изучать продвинутые функции, понимать, как они работают и писать свои версии этих функций (алгоритмы). Будем решать много разноплановых задач, с помощью которых подготовимся к участию в олимпиадах по программированию. Программа курса будет размещена в ближайшее время. Следите за обновлением информации Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование. Не секрет, что востребованность ИТ-специалистов в последние годы очень выросла. Как выбрать направление в ИТ-сфере для школьника? А что, если не просто учиться программированию, а развивать навыки работы с информацией в различных сферах? Помочь школьникам, выстроить путь в этом направлении, поможет курс «Анализ данных на Python». В этом курсе теория и практические задачи подобраны так, что ребята не только улучшают знания в области информатики, но и знакомятся с дополнительными разделами математики, теорией вероятности, математической статистикой, решают практические вопросы исследования данных в различных областях. Анализ данных на Python Профильное программирование 10 класс Курс программирования «Анализ данных на Python» рассчитан на школьников 10 классов, которые знакомы с основными понятиями программирования и хотят стать аналитиками данных. «Анализ данных на Python» — годовой курс (36 занятий по 4 академических часа), направленный на изучение и практическое использование Python-библиотек для работы с данными, на разработку моделей машинного обучения. В последнем разделе курса ученики познакомятся с технологическим процессом коллективной разработки программного обеспечения. Первый раздел курса — повторение основ Python — будет хорошей базой для тех, кто решит использовать этот язык при сдаче ЕГЭ по информатике. Все разделы курса указаны в учебном плане
. На занятиях школьники познакомятся с теорией и базовыми инструментами, которые пригодятся на всех этапах участия в Национальной олимпиаде по анализу данных DANO. График проведения олимпиады сентябрь-декабрь, поэтому логично пройти обучение на годовом курсе «Анализ данных на Python» в 2025-2026 годах, чтобы в сентябре-декабре 2026 года участвовать в олимпиаде. А это значит, что курс идеально подходит для десятиклассников. Число участников олимпиады DANO невелико (в сравнении с олимпиадами по информатике и программированию). Олимпиада вошла в Перечень олимпиад школьников Министерства науки и высшего образования Российской Федерации как профиль «Анализ данных» Всероссийской олимпиады школьников «Высшая проба». Призеры и победители олимпиады получают преимущества при подаче заявлений на направления бакалавриата и специалитета в несколько российских вузов (подробнее см. на сайте ). Зачисление на курс «Анализ данных на Python» проходит по результатам входного теста. Ссылка на входной тест — https://forms.gle/VzbafRaZiDNzKgfS9 Учебные занятия по курсу проходят в дистанционном формате на платформе Zoom. Курс обеспечен методическими материалами и домашними заданиями, выполняя которые, ребята смогут копить баллы за каждое выполненное задание! Баллы отражают уровень прогресса в обучении. Использование такой системы подготовит учеников к балльно-рейтинговой системе — форме оценивания успехов, применяемой в большинстве вузов России.
Все материалы и задания доступны на платформе дистанционного обучения Google Classroom, что в совокупности с использованием Google Colaboratory для изучения Python, делает возможным обучение с любого компьютера, подключенного к сети Интернет. Никаких дополнительных установок программного обеспечения для Python не требуется. Существенным достоинством курса является организация самостоятельной работы школьников в форме домашних заданий. Московский физико-технический институт Лаборатория по работе с одарёнными детьми Введение в современную информатику (7-8 классы)
Преподаватель курса: Куракин П.В. Суббота 10:00-12:30 (очно) Программа курса Курс проводится в очном режиме и рассчитан на полный учебный год для школьников 7 – 8 классов (2,5 часа в неделю).
Материал курса обладает высокой степенью оригинальности и аутентичности, как в своих отдельных разделах, так и их совокупности. Материал курса условно делится на 5 разделов:
Пояснения и иллюстрации по разделам:
1. Используемая литература: ü М.А. Евдокимов, «От задачек к задачкам»;
ü К.А. Кноп, «Взвешивания и алгоритмы. От головоломок к задачам»;
ü Е. Гик, «Весёлые головоломки»;
ü А. Левитин, М. Левитина, «Алгоритмические головоломки»;
ü Б. Орлин «Математические игры с дурацкими рисунками»;
ü M. Gardner, “The Colossal Book of Short Puzzles and Problems”.
2. Примеры работы школьников 7 и 8 кл. на на ЛШ МФТИ 2025 г: 8 класс, лабораторная работа на игру «Жизнь» Дж. Конуэя 7 класс, лабораторная работа на метод сортировки массива слиянием 7 класс, лабораторная работа на обход бинарного дерева 3. Оригинальный (авторский) цикл задач на Excel (включая аналогичные популярные электронные таблицы). Задачи представляют собой разработку кода для проверки возможных (подставляемых «вручную») решений различных пространственно – комбинаторных головоломок типа Судоку (а так же, её разнообразных вариаций, аналогов, близких и дальних «родственников»). Главная особенность этого раздела – интенсивное и глубокое обучение школьников понятию функции (что даёт связку со школьным курсом алгебры), и понятию структур данных. Эти два понятия являются центральными в программировании, и школьники плавно подводятся к их изучению и использованию. Сначала происходит освоение максимально широкого спектра встроенных функций Excel (что имеет понятное практическое применение), далее школьники учатся самостоятельно конструировать все более сложные (составные) функции. На этом этапе ещё не вводится понятие алгоритма обработки данных, а также не используются циклы, что позволяет сделать введение в программирование более постепенным, чем это обычно делает при «взрослом» подходе. С другой стороны - позже, когда учащиеся перейдут к использованию алгоритмов и циклов, они смогут делать это более осознанно (будут понимать, что алгоритмы и циклы используют функции и производят вычисления именно на основе структур данных). Пакет OpenSCAD не является инструментом из разряда т.н. универсальных языков программирования, однако он завоевал признание и популярность среди начинающих свой путь в программировании благодаря уникальному сочетанию своих свойств: 4. Относительно молодой язык программирования Julia был создан специально для математических расчётов, его синтаксис более простой, чем у универсальных промышленных языков программирования (типа Python) и напоминает язык системы математических расчётов MATLAB. Автоматическая генерация лабиринтов, заявленная в курсе как центральна тема для изучения языка Julia, интересна и как самостоятельная алгоритмическая задача, допускающая множество подходов, и как некоторое введение в мир искусственного интеллекта, и как один из элементов в промышленной разработке компьютерных игр. 5. Пакет NetLogo уже давно завоевал признание как в части «взрослой» (университетской, академической) исследовательской работы по моделированию самых разнообразных природных явлений, так и в обучении школьников и студентов. Примеры моделей, построенных в среде NetLogo: (И многое другое). Среда NetLogo имеет не только собственный язык, но и собственную оригинальную парадигму программирования, что значительно расширяет вычислительный кругозор учащихся. Модели, самостоятельно разработанные учащимися в NetLogo, впоследствии (в старших классах) можно использовать в проектной деятельности школьников по самым разным предметам. Для зачисления на курс необходимо прислать решения тестового задания на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. (обязательно указать фамилию ученика). Это задачи на логику, рассуждения и нестандартные способы арифметических вычислений. Для гарантированного зачисления достаточно правильно решить (и подробно описать решение) любых 4-х задач из 7. Правильного решения 3-х задач может оказаться достаточно, в зависимости от общей ситуации с набором на курс.
1. Программирование 7 класс, базовый уровень
Факультет математики и компьютерных наук. Бакалавр.
Преподаватель информатики, математики,программирования (PYTHON 3 , VBA, C#), курсов по вебу (HTML 5+CSS3).
Разработчик Python (разработка телеграм ботов, парсеров (Beautiful Soup 4, Selenium, requests, pandas,Tkinter).
Программирование на Python 3(написание парсеров с использованием библиотек: bs 4, selenium, pandas,Tkinter;
боты для телеграмм (pytelegrambot), работа с Flask, Django)
Разработка Игр (Scratch, Pencil Code, Construct 3, Unity)
Опыт работы с *nix системами
Преподаватель подготовительных курсов «Физтех-Потенциал».
Тестирование высылается после регистрации. Выполняется в письменном виде и отправляется на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
№ занятия
Тема
1
2
3
4
5
6
7
8
9
10
11
12
13
Решение задач.
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Выбор итогового проекта и начало работы над ним.
35
Работа над итоговых проектом.
36
Презентация и защита итоговых проектов.
2. Программирование 7 класс, продвинутый уровень
Тестирование высылается после регистрации. Выполняется в письменном виде и отправляется на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
3. Анализ данных на Python Профильное программирование (10 класс)
Общая трудоемкость курса «Анализ данных на Python» — 288 академических часов, из них 144 — аудиторные дистанционные занятия на платформе Zoom и 144 — выполнение домашних заданий. По окончании курса при успешной защите выпускного проекта возможна выдача сертификата МФТИ.
4. Введение в современную информатику (7-8 классы)



a) Результат выполнения любой, самой простой программы на языке OpenSCAD, представляет собой готовую 3D конструкцию на мониторе компьютера, что идеально подходит для обучения «визуалами» (подавляющее большинство людей – визуалы);
b) Разработанные учащимися конструкции можно преобразовать в форматы, пригодные для 3D-печати. Работа с 3D-принтерами не входит в программу курса, но учащиеся могут впоследствии использовать результаты своей работы где-либо ещё;
c) язык операторов и функций OpenSCAD – это текстовый язык описания 3-мерных форм, сочетающий свойства процедурного и функционального подхода в программировании, то есть – учащиеся получают первичное представление сразу о нескольких парадигмах современного программирования; так же – появляется использование циклов;
d) Работа в OpenSCADвеликолепно развивает вычислительное и математическое мышление (это не одно и то же) на естественном и наглядном материале.
e) Образование муравьиных троп;
f) Осень (динамика состояния деревьев);
g) Поиск пчёлами улья;
h) Регуляция сахара в крови;
i) Функционирование хлоропластов в клетках растений;
j) Развитие мышц;
k) Динамика опухолей;
l) Динамика вирусов;
m) Моделирование кучи песка;
n) Моделирование турбулентности;
o) Моделирование теплопроводности в материалах;
p) Фабрика роботов;
q) Транспортные пробки.
Расписание курсов
Расписание еще утверждается, возможны изменения и дополнения.
![]()
ОЧНЫЕ ЗАНЯТИЯ 2025/2026 (7-11 классы) МФТИ, г. Долгопрудный
ОЧНЫЕ ЗАНЯТИЯ 2025/2026 (7-11 классы) Московский корпус МФТИ, г. Москва
ОНЛАЙН ЗАНЯТИЯ 2025/2026 (7-11 классы)
Подготовительные курсы по школьным предметам
Дополнительные курсы подготовки
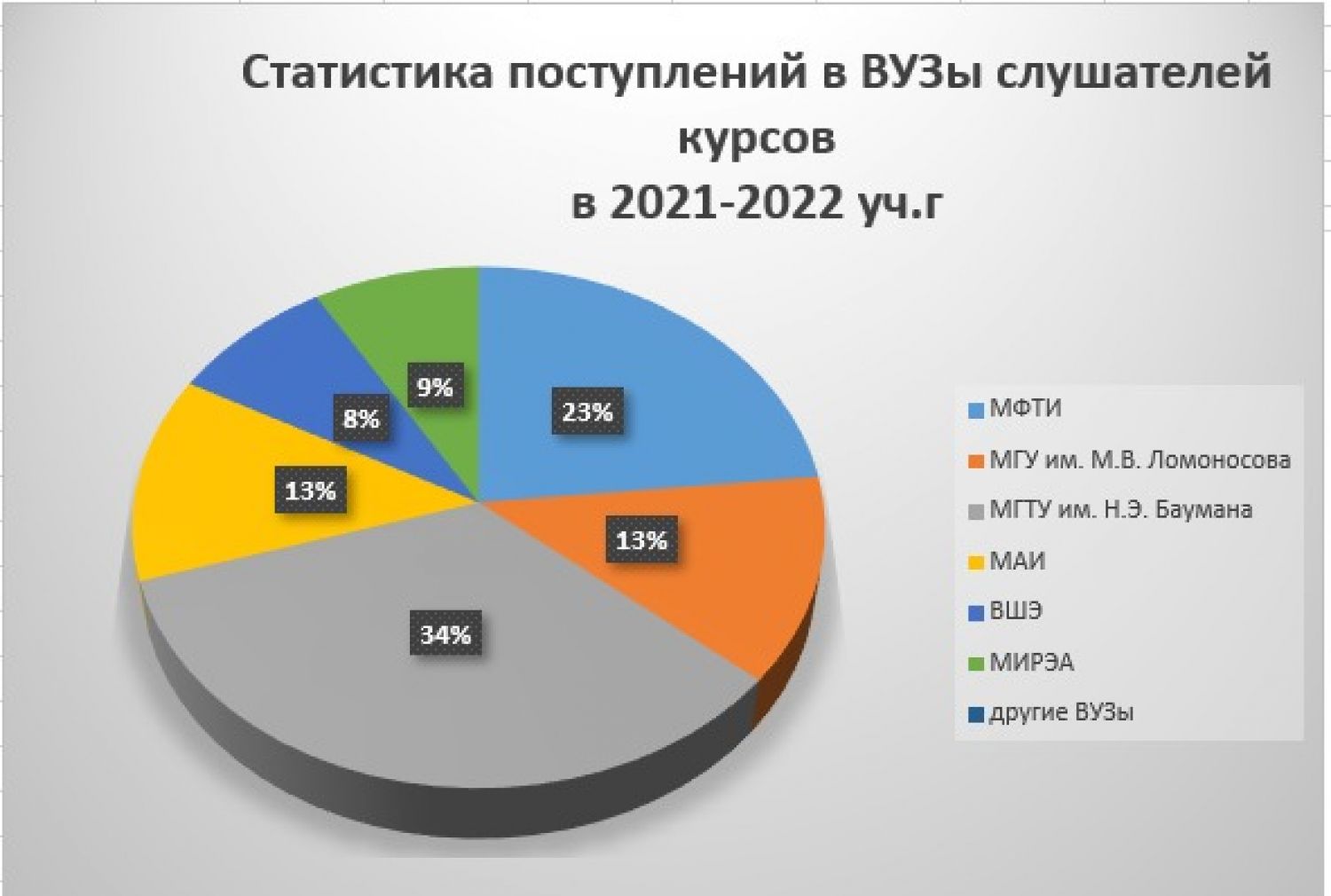
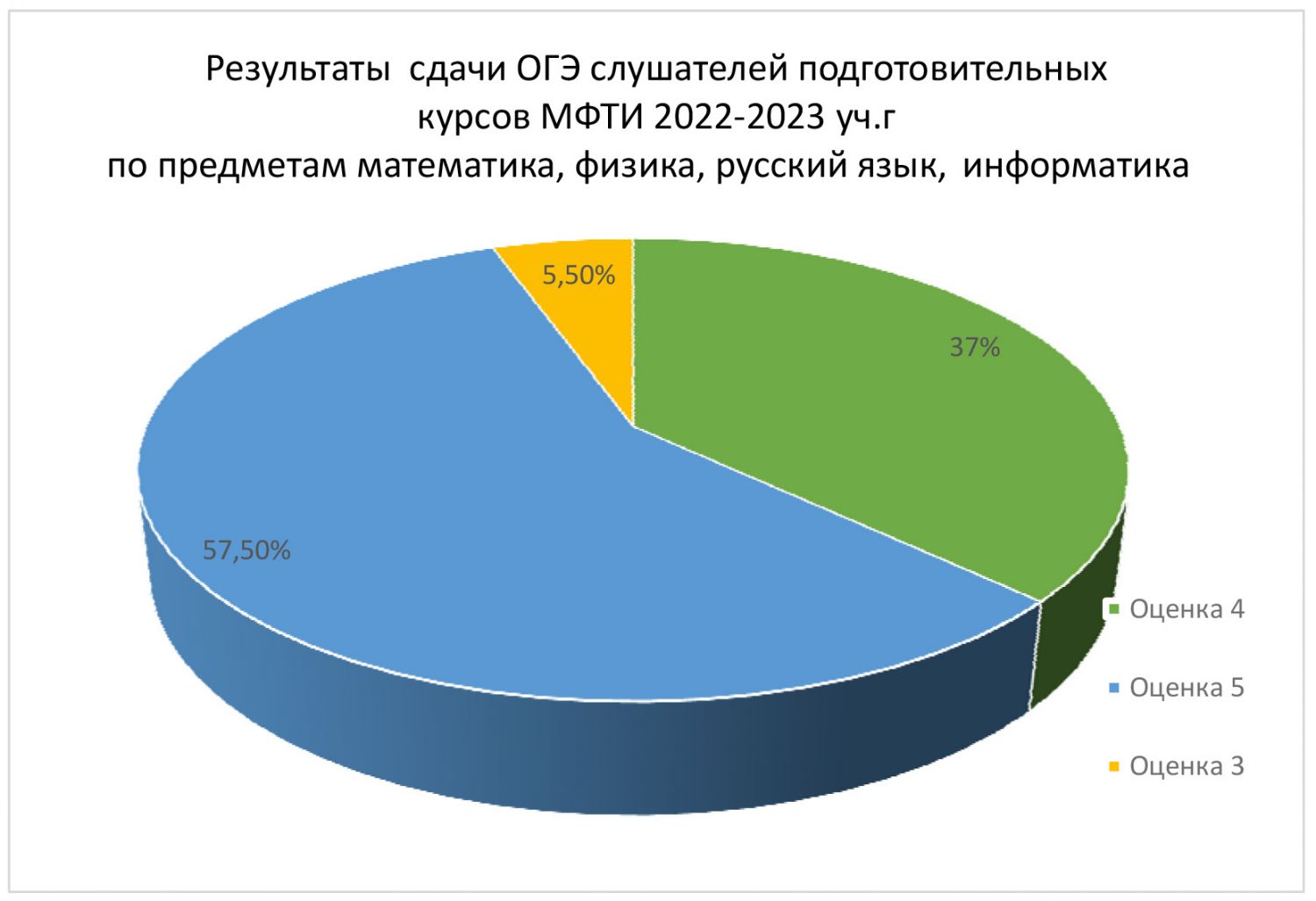
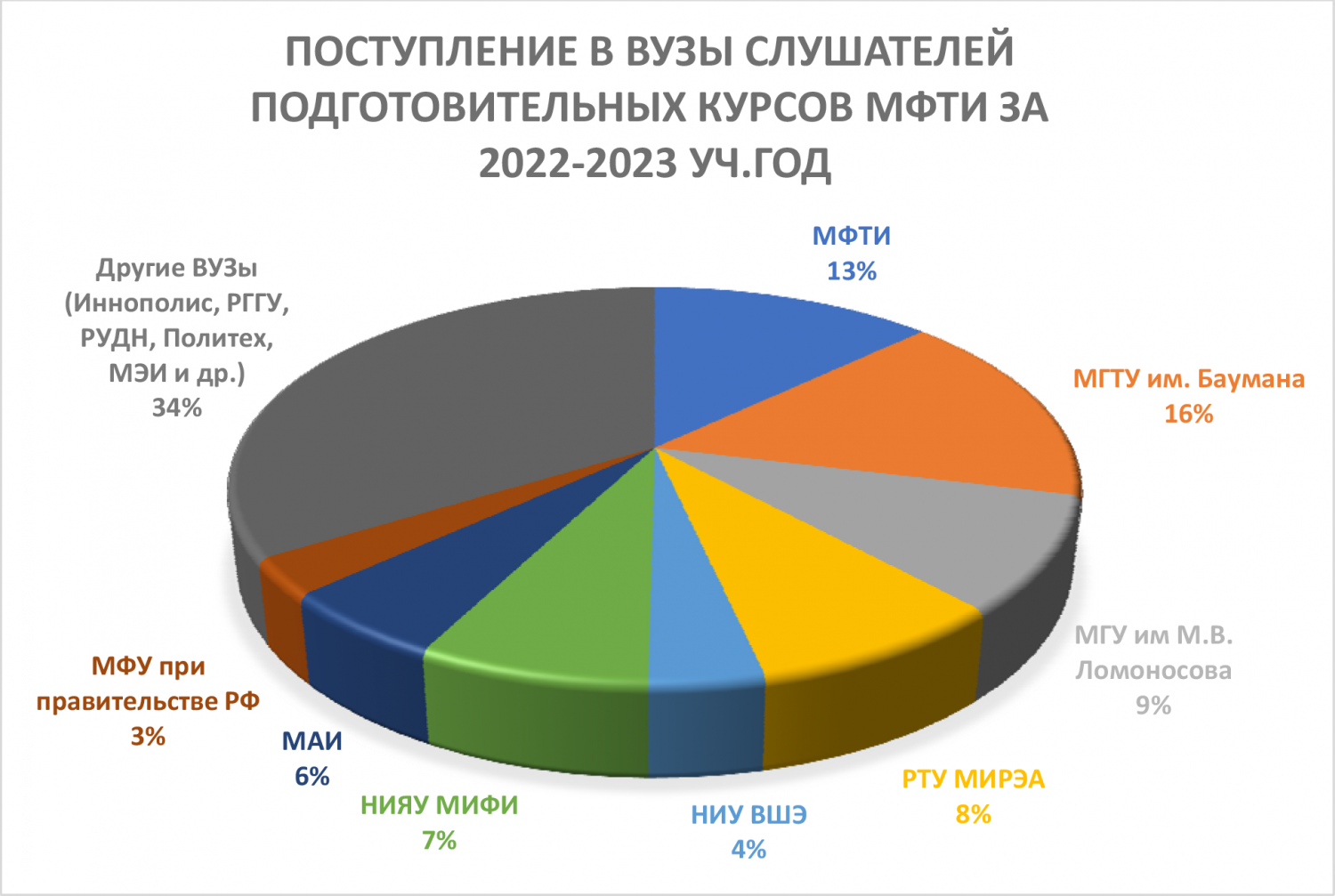
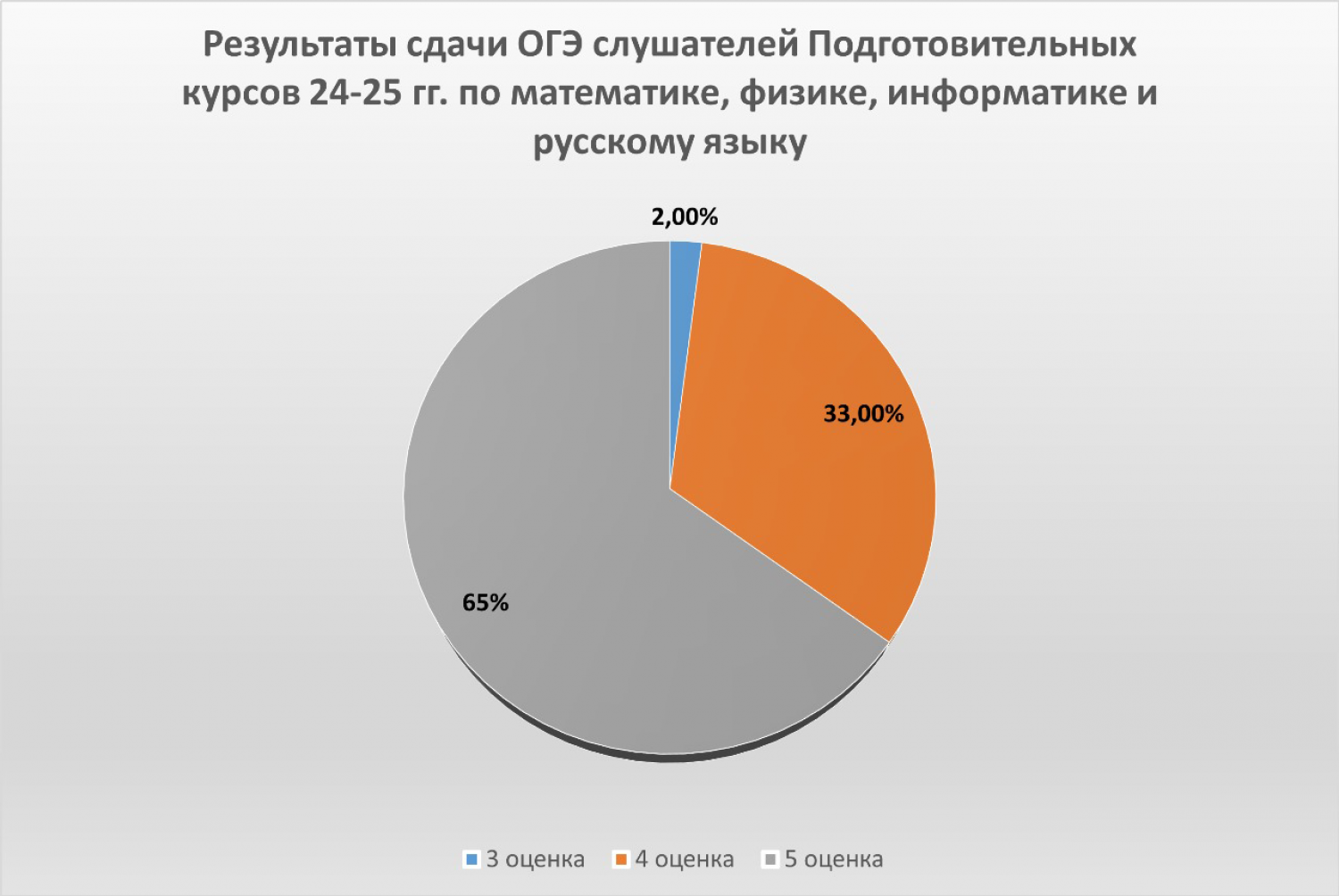
Статистика
Стоимость подготовительных курсов для школьников
|
Класс |
1 занятие |
Месяц |
Кол-во ак.ч. за 1 занятие по выбранному курсу |
|||
|
Онлайн |
Очно |
Онлайн |
Очно |
|||
|
7 класс |
1875 |
2025 |
7500 |
8100 |
2,5 |
|
|
8 класс |
2075 |
2225 |
8300 |
8900 |
3 |
|
|
7-8 классы |
2075 |
2225 |
8300 |
8900 |
3 |
|
|
9-11 классы |
2325 |
2500 |
9300 |
10000 |
4 |
|
|
|
||||||
|
|
||||||
|
ЭКСПЕРИМЕНТАЛЬНАЯ ФИЗИКА |
||||||
|
7 класс |
2025 |
8100 |
2,5 |
|||
|
8 класс |
2225 |
8900 |
3 |
|||
|
9 класс |
2500 |
10000 |
4 |
|
||
|
|
||||||
|
|
||||||
|
ПОДГОТОВКА К ПЕРЕЧНЕВЫМ ОЛИМПИАДАМ
|
|
|||||
|
10-11 классы |
2650 |
2800 |
10600 |
11200 |
4 |
|
- Стоимость за месяц включает в себя 4 занятия, без привязки к календарному месяцу. Если в месяце 5 недель, значит пятая неделя переходит на другой месяц.
- Количество занятий за 1 курс рассчитано с учетом новогодних праздничных дней.
- Занятия на курсах «Подготовка к перечневым олимпиадам 2026 (физика, математика) для 11 классов проходят с сентября по середину февраля (до заключительного этапа олимпиады). Группы 10 класса занимаются до конца апреля. После олимпиады на курсе происходит разбор ошибок.
|
Система скидок: Многодетным семьям при предъявлении свидетельства, скидка 5%. При участии на курсах от 2-х детей из одной семьи скидка 5%, скидки не суммируются. Обучение можно оплатить материнским капиталом (со второго месяца обучения). |
Как проходит обучение на подготовительных курсах?
Основная форма обучения – это семинары, на которых учащиеся тренируются в решении задач под руководством преподавателя.
Форма занятий позволяет осуществлять индивидуальную работу с учащимися. Ведется учет посещаемости занятий учащимися и учет их успеваемости, а также проверка домашнего задания.
Выполнение домашнего задания – это обязательное условие эффективного обучения. В случае систематического невыполнения – учащийся будет исключен из группы.
Занятия по каждому предмету проводятся один раз в неделю в очных группах по 10–15 человек в онлайн формате до 20 человек.
Предварительное тестирование начинается в первой декаде июля в режиме онлайн.
Программа подготовки рассчитана на 9 месяцев для профильных предметов.
Интенсивная подготовка:
- С января мы запускаем интенсивные 5-ти месячные курсы.
- С марта традиционно начинаются занятия на экспресс-курсах по подготовке к ЕГЭ учащихся 10-11 классов.
Курсы МФТИ онлайн
Если нет возможности очно посещать занятия по подготовке к ЕГЭ и поступлению, записывайте на курсы МФТИ онлайн. Зарегистрироваться на подготовительные курсы МФТИ можно прямо на сайте или по телефону 8 (495) 542-65-62.
Договор заключается с родителями или с самим учащимся, достигшим 18 лет. При заключении договора потребуется:
- паспорт лица, с которым заключается договор;
- договор необходимо предоставить не позднее 2 занятия, без договора учащиеся до занятий не допускаются.
Чтобы записаться на подготовительные курсы для школьников или задать любые дополнительные вопросы, звоните нам:
Лицензии и сертификаты
Отзывы