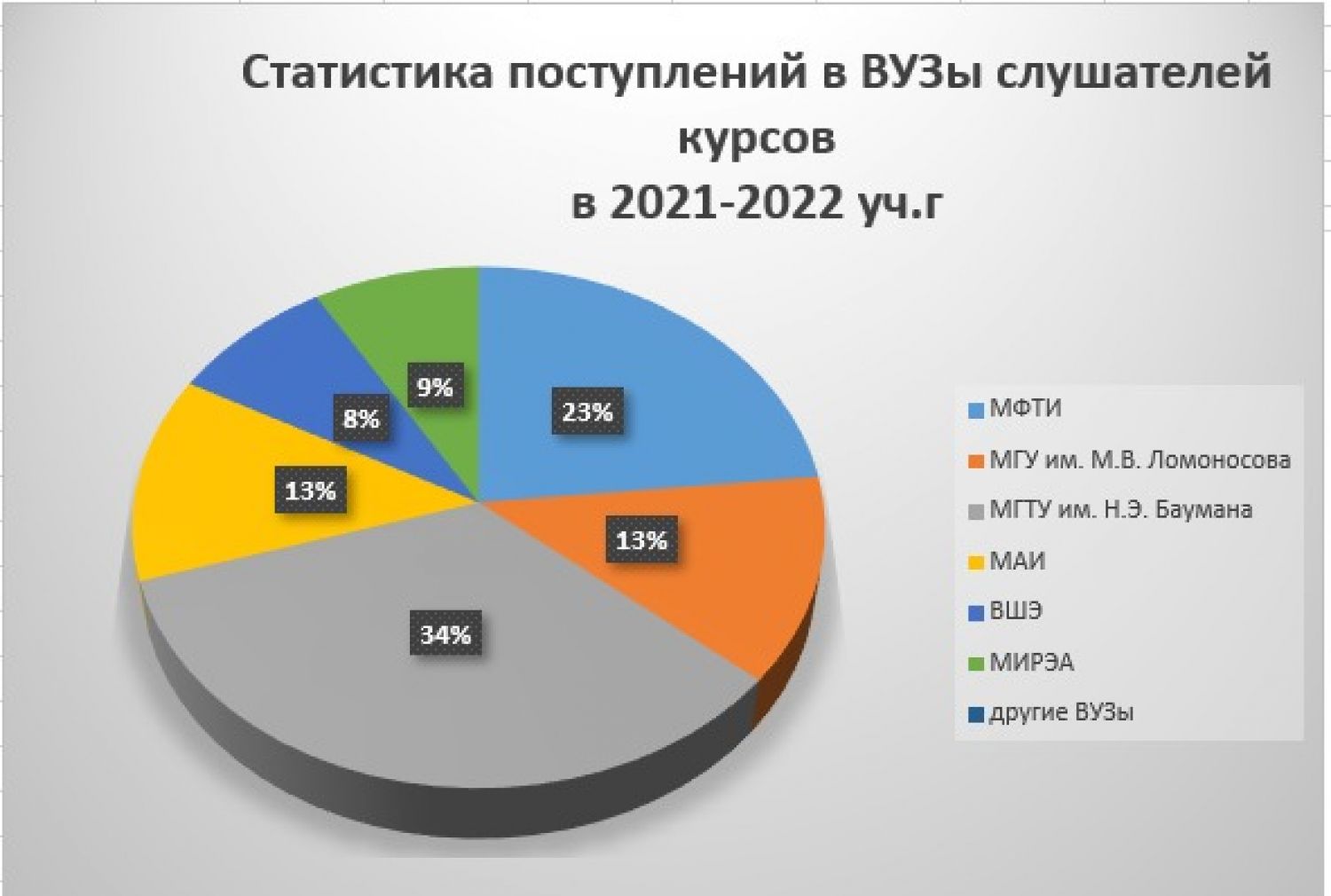
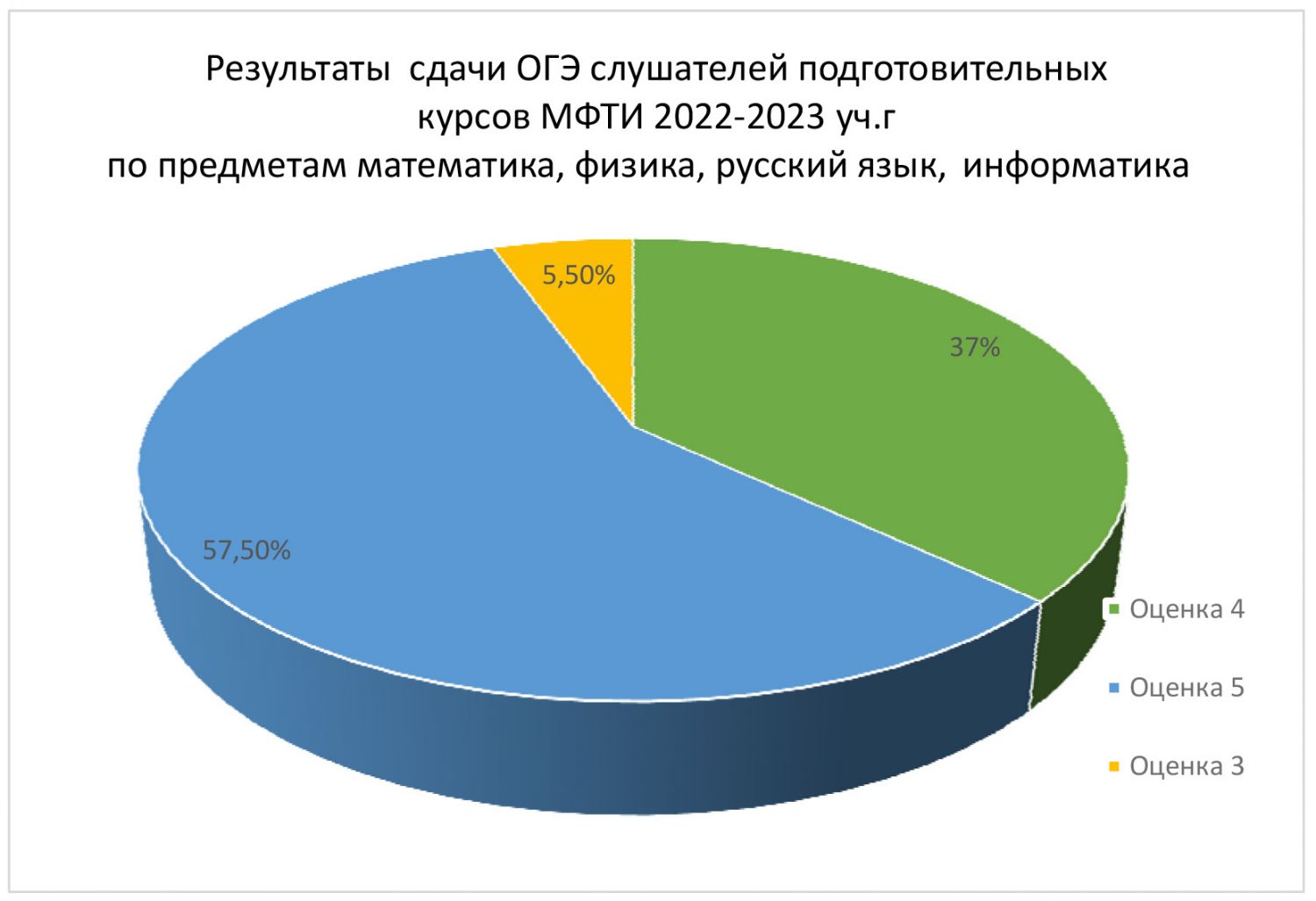
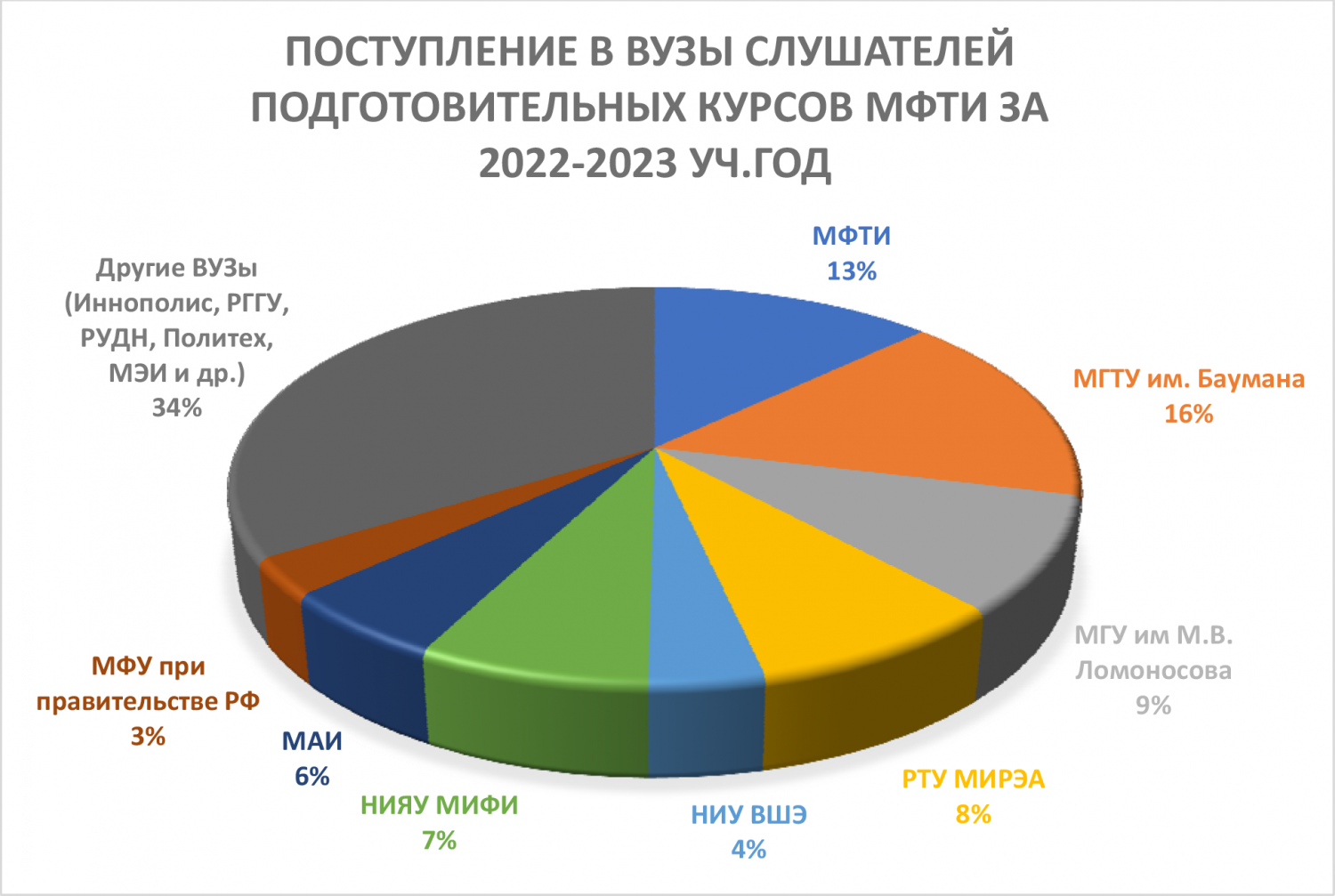
Подготовительные курсы МФТИ 2023/2024
 Регистрация на годовые курсы 2024/2025 откроется в мае.
Регистрация на годовые курсы 2024/2025 откроется в мае.
С 4 сентября приглашаем учащихся 7–11 классов на годовые подготовительные курсы по следующим предметам:
|
|
|
|
«Подготовка к заключительным этапам перечневых олимпиад I уровня 2024»
|
Как проходит обучение на подготовительных курсах?
Основная форма обучения – это семинары, на которых учащиеся тренируются в решении задач под руководством преподавателя.
Форма занятий позволяет осуществлять индивидуальную работу с учащимися. Ведется учет посещаемости занятий учащимися и учет их успеваемости, а также проверка домашнего задания.
Выполнение домашнего задания – это обязательное условие эффективного обучения. В случае систематического невыполнения – учащийся будет исключен из группы.
Занятия по каждому предмету проводятся один раз в неделю в группах по 10–15 человек
Предварительное тестирование начинается в первой декаде июля. Следите за информацией на сайте.
Программа подготовки рассчитана на 9 месяцев для профильных предметов.
Интенсивная подготовка:
с января мы запускаем интенсивные 5-ти месячные курсы.
с марта традиционно начинаются занятия на экспресс-курсах по подготовке к ЕГЭ учащихся 10-11 классов.
Следите за информацией на сайте.
Программы курсов
Для чего участвовать в олимпиадах? Многие школьники отказываются от участия в олимпиадах, так как не видят смысла тратить своё личное время на подготовку, а учителя не пытаются объяснить своим подопечным, какую выгоду те могут извлечь из интеллектуальных конкурсов. Из-за недостатка информации одаренные ребята упускают возможность поступить в престижный вуз за счет государственных средств или даже выиграть солидную денежную премию! Если школьник с первого класса участвует в олимпиадах, уже знает все их тонкости, многому научился, готовится и старается, то победить гораздо проще, чем, придя впервые на олимпиаду в 10-11 классах. Все вопросы и задачи олимпиад рассчитаны на творческое нестандартное мышление, на умение рассуждать и делать выводы, на способность самостоятельно анализировать имеющуюся информацию. Каждая олимпиада и конференция – это подобие маленького экзамена, устного или письменного. Если ребенок с первого класса может спокойно писать в незнакомой обстановке, устно отвечать не – знакомым людям, то ЕГЭ и экзамены в ВУЗе для него покажутся совсем простым и привычным делом. Конференции и устные олимпиады требуют от ребенка умения аргументировать свои ответы, не бояться устных выступлений. Еще ребенку важно знать, что он является частью некоего интеллектуального сообщества, важно иметь возможность сравнивать свои достижения с успехами других, ощущать дух соревнования.
Обычно, школьная программа не достаточно емкая и сложная. Поэтому учащиеся, освоившие школьную программу, нуждаются в дополнительном математическом и физическом образовании, что даст им возможность участвовать в Олимпиадах.
На базе подготовительных курсов МФТИ проходят курсы олимпиадной подготовки. 7 класс 1. Логика. Принцип Дирихле. Высказывания (парадокс лжеца). Таблицы истинности. Турнирные таблицы. Взвешивания и переливания. Обратный ход. Доказательство от противного. (Метод математической индукции.) Стратегии в математических играх. 2. Множества. Свойства множеств. Принцип включения/исключения. Комбинаторика. Сочетания и размещения. Перестановки. Соответствие между множествами. 3. Числа. Целые и рациональные числа. Свойства чисел. Делимость. Деление с остатком. Простые числа (решето Эратосфена). НОД, НОК и их свойства. Алгоритм Евклида поиска НОД. Линейное представление НОД. Основная теорема арифметики. Признаки делимости. Диафантовы уравнения – линейные и нелинейные. Десятичная запись числа. 4. Алгебра. Доказательства тождеств. Многочлены. Доказательство неравенств. Неравенства между средними. Числовые неравенства. (Неравенство Коши, неравенство Чебышева, транс-неравенство.) Линейные уравнения и системы линейных уравнений. Выделение полного квадрата (решение квадратного уравнения). Прямая и обратная пропорциональности и их графики. Система координат. 5. Геометрия. Признаки равенства треугольников. Отрезки в треугольнике. Свойства прямоугольных треугольников. Равнобедренный треугольник. Параллельность, удвоение медианы. Четырёхугольники – параллелограмм, ромб, квадрат. Площадь треугольника. Свойство площади. 6. Приложения. Текстовые задачи – движение, проценты и доли, смеси, стоимость, (залог/кредит), тарифы, оптимальный выбор. Классическая вероятность. Графы: степень вершины и двудольные графы. 7. Нестандартные темы и методы. Раскраски. Разрезания фигур. Ребусы. Ряды и ожерелья. Конфигурации из спичек. Конфигурации многогранников. Математические игры и стратегии. 8 класс 1. Задачи на целые чи сла 9 класс 1. Алгебра многочленов и рациональных выражений Экспресс-курс. Физика-профиль 10 класс Пятница с 17:00-20:00. Преподаватель Корнеев В.Т. Программа составлена в соответствии с Федеральным государственным образовательном стандартом среднего общего образования (ФГОС СОО). Некоторые рассматриваемые вопросы могут немного выходить за рамки базовой школьной программы. Объем часов в интенсиве примерно в 10 раз меньше, чем в учебном курсе для углубленного изучения и примерно в 4 раза меньше, чем в базовом курсе. Интенсив ориентирован на мотивированных к учебе десятиклассников. Поэтому в программе затронуты практически все вопросы курса, но в интенсиве внимание будет сосредоточено на узловых и наиболее сложных вопросах. При этом, предполагается, что среди обучающихся найдутся школьники, в знаниях которых обнаружатся пробелы по каким-либо вопросам. Поэтому обучение будет строиться ситуативно, с учетом запросов и уровня подготовки слушателей. Теория дается в виде кратких обзоров. Основное внимание уделяется задачам уровня выше среднего и сложного, в ходе решения которых отрабатываются все принципиальные вопросы теории. Обязательным является непосредственное активное участие в работе слушателей. Нужно не стесняться задавать даже самые простые вопросы, которые «всем уже понятны»: отвечать на эти вопросы труднее всего и, как показывает практика, именно «простые» вопросы бывают пропущены теми, кому «все понятно», именно эти вопросы потом приводят их зачастую к ошибкам или в тупик. Механическое движение. Относительность механического движения. Система отсчёта. Прямая и обратная задачи механики. Радиус-вектор материальной точки, его проекции на оси системы координат. Траектория. Перемещение, скорость и ускорение материальной точки, их проекции на оси системы координат. Сложение перемещений и сложение скоростей. Равномерное и равноускоренное прямолинейное движение. Зависимость координат, скорости, ускорения и пути материальной точки от времени и их графики. Свободное падение Ускорение свободного падения Движение тела, брошенного под углом к горизонту Зависимость координат, скорости и ускорения материальной точки от времени и их графики. Законы Ньютона. Закон всемирного тяготения. Эквивалентность гравитационной и инертной массы. Сила тяжести. Зависимость ускорения свободного падения от высоты над поверхностью планеты и от географической широты. Движение небесных тел и их спутников. Законы Кеплера. Первая космическая скорость. Вес тела. Вес тела, движущегося с ускорением. Сила упругости. Закон Гука. Сила трения. Сухое трение. Сила трения скольжения и сила трения покоя. Коэффициент трения. Сила сопротивления при движении тела в жидкости или газе, её зависимость от скорости относительного движения. Давление. Твёрдое тело. Поступательное и вращательное движение твёрдого тела. Момент силы относительно оси вращения. Плечо силы. Сложение сил, приложенных к твёрдому телу. Центр тяжести тела. Условия равновесия твёрдого тела. Устойчивое, неустойчивое, безразличное равновесие. Импульс материальной точки, системы материальных точек. Центр масс системы материальных точек. Импульс силы и изменение импульса . Закон сохранения импульса. Реактивное движение. 3 Работа силы на малом и на конечном перемещении. Графическое представление работы силы. Мощность силы. Кинетическая энергия материальной точки. Теорема об изменении кинетической энергии материальной точки Потенциальные и непотенциальные силы. Потенциальная энергия. Потенциальная энергия упруго деформированной пружины. Потенциальная энергия тела в однородном гравитационном поле. Потенциальная энергия тела в гравитационном поле однородного шара (внутри и вне шара). Вторая космическая скорость. Третья космическая скорость. Связь работы непотенциальных сил с изменением механической энергии системы тел. Закон сохранения механической энергии. Упругие и неупругие столкновения. Уравнение Бернулли для идеальной жидкости как следствие закона сохранения механической энергии Тема 1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории (МКТ), их опытное обоснование. Диффузия. Броуновское движение. Характер движения и взаимодействия частиц вещества. Модели строения газов, жидкостей и твёрдых тел. и объяснение свойств вещества на основе этих моделей. Масса и размеры молекул. Количество вещества. Постоянная Авогадро. Тепловое равновесие. Температура и её измерение. Шкала температур Цельсия. Модель идеального газа в МКТ: частицы газа движутся хаотически и не взаимодействуют друг с другом. Газовые законы. Уравнение Менделеева—Клапейрона Абсолютная температура (шкала температур Кельвина). Закон Дальтона. Изопроцессы в идеальном газе с постоянным количеством вещества. Графическое представление изопроцессов: изотерма, изохора, изобара. Связь между давлением и средней кинетической энергией поступательного теплового движения молекул классического идеального газа (основное уравнение МКТ идеального газа). Связь абсолютной температуры классической термодинамической системы со средней кинетической энергией поступательного теплового движения её частиц. Термодинамическая (ТД) система. Задание внешних условий для ТД системы. Внешние и внутренние параметры. Параметры ТД системы как средние значения величин, описывающих её состояние на микроскопическом уровне. Нулевое начало термодинамики. Самопроизвольная релаксация ТД системы к тепловому равновесию. Модель ТД системы в термодинамике — система уравнений: термическое и калорическое уравнения состояния. Модель классического идеального газа в термодинамике — система уравнений: уравнение Менделеева—Клапейрона и выражение для внутренней энергии. Условия применимости этой модели: низкая концентрация частиц, высокие температуры. Выражение для внутренней энергии классического одноатомного идеального газа Молярные теплоёмкости cV и cp в этой модели. Квазистатические и нестатические процессы. Элементарная работа в термодинамике. Вычисление работы по графику процесса на pV-диаграмме. Теплопередача как способ изменения внутренней энергии ТД системы без совершения работы. Конвекция, теплопроводность, излучение. Количество теплоты. Теплоёмкость тела. Удельная теплоёмкость вещества. Удельная теплота сгорания топлива. Расчёт количества теплоты при теплопередаче. Понятие об адиабатном процессе. Первый закон термодинамики. Внутренняя энергия Количество теплоты и работа как меры изменения внутренней энергии ТД системы. Второй закон термодинамики для равновесных процессов: через заданное равновесное состояние ТД системы проходит единственная адиабата. Абсолютная температура. Второй закон термодинамики для неравновесных процессов: невозможно передать теплоту от более холодного тела к более нагретому без компенсации (Клаузиус). Необратимость природных процессов. Принципы действия тепловых машин. КПД. Максимальное значение КПД. Цикл Карно. Влажность воздуха. Абсолютная и относительная влажность. Твёрдое тело. Кристаллические и аморфные тела. Анизотропия свойств кристаллов. Плавление и кристаллизация. Удельная теплота плавления. Жидкие кристаллы. Современные материалы. Деформации твёрдого тела. Растяжение и сжатие. Сдвиг. Модуль Юнга. Предел упругих деформаций. Тепловое расширение жидкостей и твёрдых тел, объёмное и линейное расширение. Преобразование энергии в фазовых переходах. Уравнение теплового баланса. Поверхностное натяжение. Коэффициент поверхностного натяжения. Капиллярные явления. Давление под искривлённой поверхностью жидкости. Тема 1. Электрическое поле Электризация тел и её проявления. Электрический заряд. Два вида электрических зарядов. Проводники, диэлектрики и полупроводники. Элементарный электрический заряд. Закон сохранения электрического заряда. Взаимодействие зарядов. Точечные заряды. Закон Кулона. Электрическое поле. Его действие на электрические заряды. Напряжённость электрического поля. Пробный заряд. Линии напряжённости электрического поля. Потенциальность электростатического поля. Разность потенциалов и напряжение. Потенциальная энергия заряда в электростатическом поле. Потенциал электростатического поля. Связь напряжённости поля и разности потенциалов для электростатического поля (как однородного, так и неоднородного). Принцип суперпозиции электрических полей. Поле точечного заряда. Однородное поле. Поле равномерно заряженной сферы. Поле равномерно заряженного шара. Поле равномерно заряженной бесконечной плоскости. Картины линий напряжённости этих полей и эквипотенциальных поверхностей. Проводники в электростатическом поле. Условие равновесия зарядов. Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора. Параллельное соединение конденсаторов. Последовательное соединение конденсаторов. Энергия заряженного конденсатора. Тема 2. Постоянный электрический ток Сила тока. Постоянный ток. Условия существования постоянного электрического тока. Источники тока. Напряжение U и ЭДС E. Закон Ома для участка цепи. Электрическое сопротивление. Зависимость сопротивления однородного проводника от его длины и площади поперечного сечения. Удельное сопротивление вещества. Последовательное, параллельное, смешанное соединение проводников. Расчёт разветвлённых электрических цепей. Правила Кирхгофа. Работа электрического тока. Закон Джоуля—Ленца. Мощность электрического тока. Тепловая мощность, выделяемая на резисторе. ЭДС и внутреннее сопротивление источника тока. Закон Ома для полной (замкнутой) электрической цепи. Мощность источника тока. Короткое замыкание. Конденсатор в цепи постоянного тока. Катушка индуктивности в цепи постоянного тока. Электрический ток в электролитах. Электролитическая диссоциация. Электролиз. Законы Фарадея для электролиза. Программа по физике для 7 класса Программа по физике для 8 класса Программа по физике для 9 класса Программа по физике для 10 класса Программа по физике для 11 класса Для чего участвовать в олимпиадах? Многие школьники отказываются от участия в олимпиадах, так как не видят смысла тратить своё личное время на подготовку, а учителя не пытаются объяснить своим подопечным, какую выгоду те могут извлечь из интеллектуальных конкурсов. Из-за недостатка информации одаренные ребята упускают возможность поступить в престижный вуз за счет государственных средств или даже выиграть солидную денежную премию! Если школьник с первого класса участвует в олимпиадах, уже знает все их тонкости, многому научился, готовится и старается, то победить гораздо проще, чем, придя впервые на олимпиаду в 10-11 классах. Все вопросы и задачи олимпиад рассчитаны на творческое нестандартное мышление, на умение рассуждать и делать выводы, на способность самостоятельно анализировать имеющуюся информацию. Каждая олимпиада и конференция – это подобие маленького экзамена, устного или письменного. Если ребенок с первого класса может спокойно писать в незнакомой обстановке, устно отвечать не – знакомым людям, то ЕГЭ и экзамены в ВУЗе для него покажутся совсем простым и привычным делом. Конференции и устные олимпиады требуют от ребенка умения аргументировать свои ответы, не бояться устных выступлений. Еще ребенку важно знать, что он является частью некоего интеллектуального сообщества, важно иметь возможность сравнивать свои достижения с успехами других, ощущать дух соревнования.
Обычно, школьная программа не достаточно емкая и сложная. Поэтому учащиеся, освоившие школьную программу, нуждаются в дополнительном математическом и физическом образовании, что даст им возможность участвовать в Олимпиадах.
На базе учебного центра «Физтех – Потенциал» проходят два курса олимпиадной подготовки. 7 класс 8 класс 1. Кинематика равномерного и кусочно-равномерного движения 7. Условия равновесия твердого тела. Центр тяжести. 11. Количество теплоты. Теплоемкость и удельная теплоемкость. 14. Электрические заряды. Закон сохранения заряда. 20. Закон прямолинейного распространения света. Тень и полутень. 9 класс 10 класс 11 класс Программа 7 класс
Уч. часов *ЛР – Лабораторная работа Примерные планы некоторых занятий 2. Основные библиотеки и команды языка PYTHON Инсталляция программной среды PYTHON Общие характеристики языка Основные библиотеки и конструкции языка Перевод алгоритма в компьютерную программу 7. Прямолинейное равномерное движение. Скорость Линейная функция y = kx + b
ее график БиблиотекиTkinter, Turtle. Оператор tracer(). Цикл for. Создание программной модели движения автомобиля. Решение задач ЕГЭ и ОГЭ с использованием программной модели. Создание программной модели движения шарика Выполнение лабораторной работы в среде дополненной реальности - измерение пройденного пути линейкой на экране - измерение времени движения шарика при помощи секундомера Программа 8 класс
Уч. часов *ЛР – Лабораторная работа Примерные планы некоторых занятий 2. Основные библиотеки и команды языка PYTHON Инсталляция программной среды PYTHON Общие характеристики языка Основные библиотеки и конструкции языка Перевод алгоритма в компьютерную программу 7. Прямолинейное равномерное движение. Скорость Линейная функция y = kx + b
ее график БиблиотекиTkinter, Turtle. Оператор tracer(). Цикл for. Создание программной модели движения автомобиля. Решение задач ЕГЭ и ОГЭ с использованием программной модели. Создание программной модели движения шарика Выполнение лабораторной работы в среде дополненной реальности - измерение пройденного пути линейкой на экране - измерение времени движения шарика при помощи секундомера Программа по русскому языку (9 класс) – с 1 октября Анализ контрольной работы. Правописание согласных в корне. Двойные согласные. Грамматическая основа предложения. Подготовка к ОГЭ: структура изложения. Правописание приставок. Односоставные предложения. Подготовка к ОГЭ: способы сжатия текста. Практическая работа. Правописание Ъ и Ь. Буквы Ы и И после приставок. Второстепенные члены предложения. Подготовка к ОГЭ: способы сжатия текста. Практическая работа. Гласные после шипящих и Ц. Обособленные обстоятельства, определения и приложения. Подготовка к ОГЭ: структура эссе. Проверочная работа по орфографии. Правописание сложных существительных. Обособление уточняющих, пояснительных и присоединительных членов предложения. Подготовка к ОГЭ: эссе. Практическая работа Суффиксы существительных. Правописание окончаний существительных. Однородные члены предложения. Обобщающие слова при однородных членах. Подготовка к ОГЭ: эссе. Практическая работа. Правописание сложных прилагательных. Однородные и неоднородные определения. Подготовка к ОГЭ: эссе. Практическая работа. Правописание прилагательных и местоимений. Обособление дополнений. Пунктуация в предложениях с союзом КАК. Подготовка к ОГЭ: собеседование (знакомство с экзаменационными материалами). Правописание глаголов (окончания, суффиксы, Ь в глагольных формах). Знаки препинания при прямой речи. Обращения, вводные слова, междометия. Подготовка к ОГЭ: собеседование (знакомство с экзаменационными материалами). Практическая работа. Правописание глаголов (окончания, суффиксы, Ь в глагольных формах). Контрольная работа по разделу «Простое предложение». Подготовка к ОГЭ: собеседование (знакомство с экзаменационными материалами). Практическая работа. Правописание причастий. Сложное предложение. Знаки препинания в сложносочиненном предложении. Анализ ошибок, допущенных учащимися в контрольной работе. Подготовка к ОГЭ: собеседование (знакомство с экзаменационными материалами). Практическая работа. Правописание Н и НН в прилагательных и причастиях. Знаки препинания в сложносочиненном предложении. Подготовка к ОГЭ: тестовая часть экзаменационной работы. Правописание Н и НН в прилагательных и причастиях. Сложноподчиненное предложение. Знаки препинания в сложноподчиненном предложении. Подготовка к ОГЭ: тестовая часть экзаменационной работы. Правописание Н и НН в прилагательных и причастиях. Сложноподчиненное предложение. Знаки препинания в сложноподчиненном предложении. Подготовка к ОГЭ: тестовая часть экзаменационной работы. Проверочная работа (правописание Н и НН в прилагательных и причастиях). Правописание наречий. Бессоюзное предложение. Знаки препинания в бессоюзном предложении. Подготовка к ОГЭ: тестовая часть экзаменационной работы. Правописание наречий. Бессоюзное предложение. Знаки препинания в бессоюзном предложении. Подготовка к ОГЭ: тестовая часть. (Проверочная работа.) Правописание имен числительных. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: изложение. (Проверочная работа.) Правописание имен числительных. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: изложение. Служебные части речи. Слитное и раздельное написание НЕ. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: изложение. (Проверочная работа.) Проверочная работа по орфографии. Слитное и раздельное написание НЕ. Различение НЕ и НИ. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: эссе. Слитное и раздельное написание НЕ. Различение НЕ и НИ. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: эссе. (Проверочная работа.) Правописание производных союзов и предлогов. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ОГЭ: анализ экзаменационных материалов. Правописание производных союзов и предлогов. Языковые средства выразительности. Контрольная работа по разделу «Сложное предложение». Подготовка к ОГЭ: анализ экзаменационных материалов. Обобщающее повторение изученного (орфография). Анализ ошибок, допущенных учащимися в контрольной работе. Подготовка к ОГЭ: анализ экзаменационных материалов. Проверочная работа по разделу «Орфография». Подготовка к ОГЭ: анализ экзаменационных материалов. Контрольная работа в формате ОГЭ. Обобщающее повторение изученного. Подготовка к ОГЭ: анализ экзаменационных материалов Программа по русскому языку (10-11 класс) Анализ контрольной работы. Орфоэпические нормы. Правописание согласных в корне. Двойные согласные. Грамматическая основа предложения. Подготовка к ЕГЭ: структура эссе. Правописание приставок. Орфоэпические нормы. Подготовка к ЕГЭ: структура эссе. Практическая работа (написание комментария). Информационная обработка письменных текстов различных стилей и жанров. Правописание Ъ и Ь. Буквы Ы и И после приставок. Синтаксические нормы. Подготовка к ЕГЭ: структура эссе: комментарий. Практическая работа. Средства связи предложений в тексте. Гласные после шипящих и Ц. Обособленные обстоятельства, определения и приложения. Подготовка к ЕГЭ: структура эссе: комментарий. Лексическое значение слова. Проверочная работа по орфографии. Слитное, дефисное и раздельное написание слов. Обособление уточняющих, пояснительных и присоединительных членов предложения. Подготовка к ЕГЭ: эссе. Лексические нормы (употребление слов в соответствии с точным лексическим значением и требованием лексической сочетаемости). Суффиксы существительных. Правописание окончаний существительных. Однородные члены предложения. Обобщающие слова при однородных членах. Подготовка к ЕГЭ: эссе. Морфологические нормы. Правописание суффиксов различных частей речи. Однородные и неоднородные определения. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание личных окончаний глаголов и суффиксов причастий. Обособление дополнений. Пунктуация в предложениях с союзом КАК. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание НЕ и НИ. Знаки препинания при прямой речи. Обращения, вводные слова, междометия. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание –Н- и –НН- в различных частях речи. Контрольная работа по разделу «Простое предложение». Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Сложное предложение. Знаки препинания в сложносочиненном предложении. Анализ ошибок, допущенных учащимися в контрольной работе. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Проверочная работа (правописание Н и НН в прилагательных и причастиях). Знаки препинания в сложносочиненном предложении. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Проверочная работа (правописание личных окончаний глаголов и суффиксов причастий). Сложноподчиненное предложение. Знаки препинания в сложноподчиненном предложении. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Речь. Языковые средства выразительности. Сложноподчиненное предложение. Знаки препинания в сложноподчиненном предложении. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание наречий. Бессоюзное предложение. Знаки препинания в бессоюзном предложении. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание наречий. Бессоюзное предложение. Знаки препинания в бессоюзном предложении. Подготовка к ЕГЭ: тестовая часть. (Проверочная работа.) Правописание имен числительных. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Лексические нормы. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Текст как речевое произведение, смысловая и композиционная целостность текста. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Функционально-смысловые типы речи. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ЕГЭ: проверочная работа. Средства связи предложений в тексте. Знаки препинания в предложениях с несколькими видами связи. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Правописание производных союзов и предлогов. Обобщающее повторение (синтаксис и пунктуация). Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Обобщающее повторение (орфография). Контрольная работа по разделу «Сложное предложение». Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Контрольная работа по разделу «Орфография». Анализ ошибок, допущенных учащимися в контрольной работе. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Обобщающее повторение изученного. Анализ ошибок, допущенных учащимися в контрольной работе. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Обобщающее повторение изученного. Подготовка к ЕГЭ: разбор варианта экзаменационной работы. Информатика 8 класс
Открыта регистрация на новый годовой курс — «Информатика» для учащихся 8 класса.
Умение находить и составлять алгоритм решения и реализовать его с помощью компьютерных систем — необходимое условие подготовки современных школьников. Это не только начало подготовки к будущей профессиональной деятельности, но и формирование новых обще-интеллектуальных умений и навыков. Курс «Информатика» способствует совершенствованию и развитию важнейших знаний и умений в области информатики и программирования, поможет более осознанно выбрать профиль дальнейшего обучения и развить алгоритмическое мышление. На курсе учащиеся Вопросы, рассматриваемые в программе, выходят за рамки обязательного содержания. Преподаватель курса Учитель информатики и программирования в рейтинговой школе Москвы (ТОП-20). Программа курса 1. История развития компьютеров (1ч) 2. Устройство компьютера (1ч) 3. Архитектура процессора (1ч) 4. Системы счисления и их виды (1ч) 5. Системы счисления с основаниями 2, 8, 16 (1ч) 6. Арифметические операции в системах счисления (2ч) 7. Кодирование и декодирование информации (2ч) 8. Основы логики (1ч) 9. Составные логические выражения (1ч) 10. Логические операции над множествами (1ч) 11. Логические элементы и схемы (1ч) 12. Ориентированные и взвешенные графы (1ч) 13. Алгоритмы на графах (1ч) 14. Разновидности языков программирования. Язык программирования Python. Синтаксис языка. Типы данных. (1ч) 15. Выражения. Операции. Порядок выполнения операций (1ч) 16. Математические операции. Генерация случайных чисел (1ч) 17. Циклы с предусловием (1ч) 18. Циклы с постусловием (1ч) 19. Функции и их аргументы (2ч) 20. Списки и кортежи (2ч) 19. Работа со строками: индексы и срезы (2ч) 20. Массивы и основные операции с ними (1ч) 21. Индексы элементов, изменение массива, срезы (1ч) 22. Два типа циклов по массиву (1ч) 23. Язык программирования C++. Возможности и синтаксис. Библиотека TX. Library (1ч) 24. Типы данных. Команды ввода и вывода данных. Арифметические операции (1ч) 25. Обработка целых, вещественных и случайных чисел. Ветвления (1ч) 26. Циклы с условием (2ч) 27. Процедуры. Процедуры с параметрами. Рефакторинг. (1ч) 28. Безопасность данных (1ч) Зачисление на курс - по результатам тестирования. Информатика 9 класс
Тестирование:
Для учащихся 9 классов входного тестирования не будет.
Помимо тем подготовки к ОГЭ и решению базовых и олимпиадных задач, данная программа дополнена техническим изучением hardware («компьютерного железа») и software (программное обеспечение), для того, чтобы в 99% случаев учащийся мог самостоятельно все сделать, не вызывая специалиста.
Компьютерная грамотность. Процессор. Что такое процессор и как он работает. Информатика. ОГЭ. Количественные параметры информационных объектов. Компьютерная грамотность. Процессор. Виды и архитектура процессоров. Информатика. ОГЭ. Кодирование и декодирование информации. Компьютерная грамотность. Материнская плата. Что такое материнская плата, как работает, виды и форматы. Информатика. ОГЭ. Значение логического выражения Компьютерная грамотность. Материнская плата. Что такое материнская плата, как работает, виды и форматы плат. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Информатика. ОГЭ. Формальное описание реальных объектов и процессов. Компьютерная грамотность. Видеокарта. Что такое видеокарта, как работает, виды и различия. Информатика. ОГЭ. Простой линейный алгоритм для формального исполнителя. Компьютерная грамотность. Видеокарта. Что такое видеокарта, как работает, виды и различия. Информатика. ОГЭ. Программа с условным оператором. Компьютерная грамотность. Накопители информации. Что такое hdd и sdd, как работает, виды и различия. Компьютерная грамотность. Сборка ПК. Как правильно подобрать и разместить все компоненты для полноценной системы с нуля. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Информатика. ОГЭ. Запросы для поисковых систем с использованием логических выражений. Компьютерная грамотность. Операционные системы. Что такое операционные системы, виды систем и их различия. Информатика. ОГЭ. Анализирование информации, представленной в виде схем. Компьютерная грамотность. Операционные системы. Создание загрузочной флешки и подбор правильного дистрибутива. Информатика. ОГЭ. Использование поиска операционной системы и текстового редактора. Компьютерная грамотность. Операционные системы. Чистая установка ОС Windows. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Компьютерная грамотность. Операционные системы. Тонкая настройка ОС Windows. Информатика. ОГЭ. Использование поисковых средств операционной системы. Компьютерная грамотность. Операционные системы. Разбор полезных программ и твиков для ОС Windows. Информатика. ОГЭ. Создание презентации. Компьютерная грамотность. Операционные системы. Чистая установка ОС Linux. Информатика. ОГЭ. Форматирование текста. Компьютерная грамотность. Операционные системы. Тонкая настройка ОС Linux. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Компьютерная грамотность. Операционные системы. Разбор полезных программ и твиков для ОС Linux. Информатика. ОГЭ. Обработка большого массива данных. Компьютерная грамотность. Операционные системы. Основы работы в терминале. Почему это быстро и удобно. Информатика. ОГЭ. Короткий алгоритм в различных средах исполнения. Компьютерная грамотность. Операционные системы. Установка нескольких операционных систем на одном ПК. Информатика. ОГЭ. Сравнение чисел в различных системах счисления. Компьютерная грамотность. Операционные системы. Основы работы в терминале. Почему это быстро и удобно. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Компьютерная грамотность. Операционные системы. Работа с виртуальными машинами. Программирование. Python. Ввод и вывод данных с помощью функций input() и print(). Переменные и типы данных. Операции с числами. Программирование. Python. Операции сравнения. Логические операции. Программирование. Python. Условная конструкция if. Программирование. Python. Операции со строками. Методы форматирования строк. Программирование. Python. Работа с циклом while. Программирование. Python. Работа с циклом for. Функция range(). Модуль random. Программирование. Python. Введение в функции. Программирование. Python. Функции с определённым и неопределённым количеством параметров. Программирование. Python. Область видимости переменных. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Программирование. Python. Знакомство со структурами данных. Списки. Программирование. Python. Знакомство со структурами данных. Словари. Программирование. Python. Знакомство со структурами данных. Множества. Программирование. Python. Работа с файлами. Функции read(), readln(), write(), writeln(). Программирование. Python. Работа с файлами. Контекстный менеджер with. Информатика. ОГЭ. Срез. Проверочная работа на основе полученных знаний. Анализ ошибок. Закрепление пройденных тем. Информатика ЕГЭ 10-11 класс. Базовый
Поурочный план занятий
Учащимся 10-11 классов необходимо выполнить тестирование для распределения в базовую или профильную группы.
Тестирование высылается после регистрации. Анализ информационных моделей. Соотношение таблицы и графа, поиск оптимального маршрута по таблице. Базы данных и файловая система. Анализ таблиц и поиск информации по параметрам. Построение таблиц истинности логических выражений. Разбор функций с применением правил логических выражений и построение таблиц. Кодирование и декодирование информации. Анализ программ (чтение кода и понимание принципов его работы). Анализ и построение алгоритмов для исполнителей. Исполнители на плоскости. Арифмометры. Посимвольное десятичное преобразование. Передача информации. Передача файлов. Сравнение нескольких способов передачи. Определить размер файла. Срез. Проверочная работа на основе полученных данных. Анализ ошибок. Работа с таблицами (Excel). Поиск символов в текстовом редакторе. Срез. Проверочная работа на основе полученных данных. Анализ ошибок. Выполнение алгоритмов для исполнителей. Исполнители Редактор, Чертёжник, условные операторы. Поиск путей в графе. Кодирование чисел. Системы счисления. Преобразование логических выражений. Множества. Числовые отрезки. Координатная плоскость. Побитовая конъюнкция. Срез. Проверочная работа на основе полученных данных. Анализ ошибок. Проверка на делимость. Робот-сборщик. Срез. Проверочная работа на основе полученных данных. Анализ ошибок. Срез. Проверочная работа на основе полученных данных. Анализ ошибок. Срез. Проверочная работа на основе полученных данных. Анализ ошибок.
Информатика ЕГЭ 10-11 класс. Продвинутый
Поурочный план занятий
Учащимся 10-11 классов необходимо выполнить тестирование для распределения в базовую или профильную группы. Тестирование высылается после регистрации. Построение таблиц истинности логических выражений. Кодирование и декодирование информации. Анализ и построение алгоритмов для исполнителей. Срез. Проверочная работа на основе полученных данных. Анализ ошибок.
Срез. Проверочная работа на основе полученных данных. Анализ ошибок.
Выполнение алгоритмов для исполнителей. Преобразование логических выражений.
Тестирование:
Для учащихся 9 классов входного тестирования не будет. Учащимся 10-11 классов необходимо выполнить онлайн тестирование для распределения в базовую или профильную группы.
![]()
Математика
7 класс
1. Дроби. Действия с дробями.
2. Модуль числа. Геометрический смысл модуля.
3. Множество. Элементы множества. Подмножество.
4. Определение степени с натуральным показателем. Умножение и деление степеней.
5. Одночлен. Действия с одночленами. Тождества.
6. Многочлен. Вычисления значений многочлена и его стандартный вид. Действия с многочленами.
7. Уравнения. Корни линейных уравнений с одной переменной. Решение задач с помощью уравнений.
8. Разложение на множители. Доказательство тождеств. Решение уравнений.
9. Функция. Формула. Вычисление значений функции по формуле. График функции. Взаимное расположения графиков функций.
10. Линейные уравнения с двумя переменными и их графики.
11. Системы уравнений. Способы решения систем уравнений. Графический способ. Решение задач с помощью систем уравнений.
12. Начальные геометрические понятия. Прямая, точка, луч, отрезок. Углы. Измерение углов.
13. Признаки параллельности двух прямых. Аксиома параллельных прямых.
14. Вектор. Виды и равенство векторов. Действия с векторами. Проекция вектора на ось координат.
15. Треугольники. Признаки равенства треугольников.
16. Соотношения между сторонами и углами треугольника. Прямоугольный треугольник.
17. Окружность. Длина и площадь окружности. Шар.
18. Элементы комбинаторики. Подсчет числа вариантов. Комбинации с повторениями. Статистические характеристики.
19. Вероятность наступления событий. Классическая схема определения вероятности.
8 класс
1. Одночлены. Многочлены. Действия с многочленами. Формулы сокращенного умножения. Преобразования выражений.
Степень с натуральным показателем.
2. Функция. Формула. Вычисление значений функции по формуле. График функции.
3. Квадратные корни. Приближенное извлечение арифметических квадратных корней. Точные и приближенные значения.
Функция y = x1/2 и ее график.
4. Преобразования выражений, содержащих корень.
5. Функция y = 1/x и ее график. Квадратичная функция и ее график.
6. Квадратные уравнения. Метод выделения полного квадрата.
7. Модуль числа.
8. Линейная функция. График линейной функции. График модуля линейной функции.
9. Параметры в уравнениях.
Логический перебор в задачах с параметром.
10. Элементы теории чисел.
11. Делимость. Признаки делимости. Простые и составные числа. Основная теорема арифметики.
12. Разложение на простые множители. Наибольший общий делитель (НОД). Наименьшее общее кратное (НОК).
14. Треугольники. Задача о делении отрезка.
15. Фигуры на плоскости. Площадные соображения.
9 класс
1. Рациональные уравнения. Отбор корней. Область допустимых значений (ОДЗ). Эквивалентные переходы. Квадратные уравнения.
Биквадратные уравнения. Кубические уравнения.
2. Параметры в рациональных уравнениях. Логический перебор в задачах с параметром. Параметры в квадратных уравнениях.
3. Прямоугольный треугольник. Медианы, биссектрисы и высоты в треугольнике. Формулы площади треугольника.
4. Рациональные неравенства. Метод интервалов.
5. Параметры в рациональных уравнениях и неравенствах.
6. Трапеция.
7. Системы нелинейных уравнений.
8. Решение задач с помощью систем уравнений.
9. Иррациональные уравнения. ОДЗ в иррациональных уравнениях. Эквивалентные переходы.
10. Уравнения с модулем.
11. Иррациональные неравенства. Неравенства с модулем.
11. Четырехугольники.
12. Параметры в иррациональных уравнениях и неравенствах.
13. Задачи о делении отрезка
14. Множества. Высказывания. Теоремы.
15. Множества на плоскости.
16. Площадные соображения при решении планиметрических задач.
17. Числовая последовательность. Арифметическая и геометрическая прогрессии.
18. Окружности.
19. Разные задачи по планиметрии.
10 класс
1. Разложение многочлена на множества. Кубические уравнения. Рациональные уравнения. Рациональные неравенства.
Метод интервалов. Иррациональные уравнения. Уравнения с модулем.
2. Метод рационализации для иррациональных неравенств и неравенств с модулем.
3. Куб. Призма. Параллелепипед. Пирамида. Сечения в стереометрии.
4. Геометрические идеи при решении задач с параметрами.
5. Функции и их свойства. Обратная функция. Четность, периодичность.
6. Перпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах.
7. Тригонометрические функции. Тригонометрическая окружность. Основные тригонометрические формулы.
8. Тригонометрические уравнения.
9. Отбор корней в тригонометрических уравнениях.
10. Планиметрия. Теоремы синусов и косинусов.
11. Различные стереометрические задачи на темы: сечения, перпендикулярность прямых и плоскостей.
12. Системы тригонометрических уравнений.
13. Тригонометрические неравенства.
14. Обратные тригонометрические функции.
15. Площадные соображения при решении геометрических задач на плоскости.
16. Угол между скрещивающимися прямыми. Угол между прямой и плоскостью.
Расстояние между скрещивающимися прямыми.
17. Числовая последовательность. Предел последовательности.
18. Производная.
19. Векторы.
11 класс
1. Показательные функции. Показательные уравнения.
2. Логарифмы. Логарифмические уравнения.
3. Угол между скрещивающимися прямыми. Угол между прямой и плоскостью.
Расстояние между скрещивающимися прямыми.
4. Решение кубических рациональных уравнений. Рациональные неравенства. Метод интервалов.
Метод рационализации в неравенствах с модулем, с корнем, а также в показательных и логарифмических неравенствах.
6. Векторы и координаты в пространстве. Решение стереометрических задач координатным методом.
Векторный способ решения стереометрических задач.
7. Сфера. Шар. Цилиндр. Конус.
9. Вписанные и описанные сферы.
10. Системы уравнений; рациональные и иррациональные неравенства (в том числе и задачи с параметром).
11. Сечения, перпендикулярность прямых и плоскостей.
12. Повторение: тригонометрические уравнения и неравенства, показательные и логарифмические уравнения и неравенства
(в том числе и задачи с параметром).
13. Решение планиметрических задач с использованием алгебраических и тригонометрических методов.
14. Элементы теории чисел. Делимость. Признаки делимости. Простые и составные числа. Основная теорема арифметики.
Разложение на простые множители.
15. Элементы финансовой математики.
Экспресс-курс. Математика
10 класс. Экспресс-курс.
1. Целые и рациональные уравнения. Замена переменной.
2. Рациональные неравенства. Метод интервалов.
3. Уравнения и неравенства с модулем.
4. Уравнения с радикалом. Метод равносильных переходов.
5. Неравенства с радикалами. Метод равносильных переходов.
6. Текстовые задачи (проценты, движение, работа, стоимость).
7. Показательные и логарифмические уравнения.
8. Показательные и логарифмические неравенства.
9. Прямоугольный треугольник. Медиана, высота. Вычисление треугольников.
10. Метод площадей.
11. Четырёхугольники (трапеция, параллелограмм, ромб)
12. Вписанная и описанная окружности.
13.Тригонометрия. Определение и тождества.
14.Тригонометрия. Формулы и уравнения.
15. Обратные триг.функции.
16. Прогрессия арифметическая.
17. Прогрессия геометрическая. Две прогрессии.
18. Признаки параллельности и перпендикулярности прямых и плоскостей. Теорема о трёх перпендикулярах.
19. Сечение многогранников. Метод следов.Олимпиадная математика
2. Буквенные выражения
3. Алгебра многочленов и рациональных выражений
4. Многоугольники и их свойства
5. Теорема Пифагора
6. Теорема Чевы и Менелая
7. ГМТ, построение циркулем и линейкой
8. Линейные операции над векторами
9. Введение в тригонометрию
2. Уравнения, неравенства и их системы
3. Задачи с параметром
4. Построение графиков функций и фигур на плоскости
5. Основы тригонометрии
6. Векторы
7. Окружность и круг
8. ГМТ, построение циркулем и линейкой
9. Преобразование плоскости
Геометрия
Экспресс-курс. Физика
МЕХАНИКА
№ занятия
Час.
Тема 1. Кинематика
1
3
2
3
Криволинейное движение. Движение материальной точки по окружности. Угловая и линейная скорость точки. Период и частота обращения Центростремительное (нормальное) и касательное (тангенциальное) ускорение точки.
Тема 2. Динамика
3
3
4
3
Тема 3. Статика твёрдого тела
5
3
Тема 4. Законы сохранения в механике
6
3
7
8
3
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
9
3
Тема 2. Термодинамика. Тепловые машины
10
3
11
3
12
3
13
3
ЭЛЕКТРОДИНАМИКА
14
3
15
3
16
3
17
3
18
3
Физика
Месяц
№
Тема занятия
1
Физические величины, измерение физических величин. Единицы измерения величин.
2
Точность и погрешность измерений. Экспериментальное задание.
3
Механическое движение. Скорость, расчёт пути и времени движения.
4
Средняя скорость движения.
5
Графический метод решения задач в механике.
6
Относительность механического движения.
7
Взаимодействие тел. Инерция. Масса и плотность вещества. Решение задач на плотность вещества.
8
Экспериментальное задание на определение плотности вещества.
9
Повторение. Решение задач на механическое движение и плотность вещества.
10
Силы в природе. Сила тяжести и вес тела. Решение задач на силу тяжести и вес тела.
11
Силы в природе. Силы упругости. Динамометр.
12
Силы в природе. Силы трения. Трение покоя и скольжения. Сложение сил.
13
Решение задач по теме: «Силы в природе».
14
Экспериментальная задача по теме «Силы в природе».
15
Давление твёрдых тел.
16
Давление жидкостей и газов. Сообщающиеся сосуды. Расчёт давления на дно и стенки сосуда.
17
Атмосферное давление. Решение задач на атмосферное давление.
18
Закон Паскаля. Гидравлический пресс.
19
Архимедова сила. Условия плавания тел. Воздухоплавание.
20
Экспериментальное задание по гидростатике.
21
Повторение. Решение задач по гидростатике.
22
Механическая работа, мощность.
23
Простые механизмы. Блок, рычаг. Правило рычага. Момент силы.
24
Экспериментальное задание на правило рычага.
25
«Золотое правило» механики. КПД простых механизмов.
26
Центр тяжести тела, условия равновесия тел.
27
Экспериментальное задание на определение центра тяжести тела.
28
Механическая энергия.
29
Закон сохранения энергии.
30
Повторение. Решение задач по теме: «Работа, мощность, энергия».
31
Повторение. Решение задач по курсу физики 7 класса.
32
Повторение. Решение задач по курсу физики 7 класса.
2. Средняя скорость и средняя плотность.
3. Векторы в физике. Сложение векторов.
4. Относительность скоростей.
5. Траектория тела. Зависимость координаты и скорости тела от времени.
6. Тепловые явления. Температура. Внутренняя энергия.
Теплопроводность. Количество теплоты. Теплоемкость.
7. Удельная теплота сгорания. Агрегатные состояния вещества. Удельная теплота плавления. Удельная теплота парообразования.
8. Тепловой баланс.
9. Влажность. Абсолютная и относительная влажность воздуха.
10. Электрические явления. Электрический заряд. Закон сохранения заряда.
11. Проводники и диэлектрики.
12. Постоянный ток. Электрические цепи. Источники тока.
Напряжение. Амперметр. Вольтметр. Сопротивление. Параллельное и последовательное соединение проводников.
13. Работа и мощность тока. Тепловое действие тока. Закон Джоуля-Ленца.
14. Оптика. Закон прямолинейного распространения света. Закон отражения. Построение изображения в плоском зеркале.
15. Закон преломления света. Полное внутреннее отражение.
1.1 Кинематика материальной точки
1.2 Прямолинейное равнопеременное движение
1.3 Равномерное движение тела по окружности
2 Динамика и законы сохранения в механике
2.1 Законы Ньютона
2.2 Закон сохранения энергии
2.3 Закон сохранения импульса
2.4 Колебательные и волновые процессы, звук
3 Тепловые явления
3.1 Строение вещества, молекулярная теория
3.2 Тепловые явления
3.3 Фазовые переходы
4 Электрические и магнитные явления
4.1 Электризация тел
4.2 Постоянный ток
4.3 Магнетизм
5 Оптика
5.1 Геометрическая оптика
6 Квантовые явления
7 Основы проведения экспериментальных работ
2. Динамика. Силы. Законы Ньютона.
3. Центростремительное ускорение. Движение тела по окружности.
4. Импульс. Закон изменения импульса. Закон сохранения импульса.
5. Молекулярно-кинетическая теория. Идеальный газ.
6. Уравнение состояния идеального газа. Внутренняя энергия. Температура.
7. Изопроцессы. Адиабатический процесс.
8. Работа в термодинамике. Циклы. КПД циклов.
9. Первый закон термодинамики.
10. Теплоемкость. Молярная теплоемкость.
11. Закон сохранения в термодинамике.
12. Электрическое поле. Закон Кулона.
13. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии.
14. Потенциал. Разность потенциалов. Напряжение.
15. Напряженность и потенциал поля равномерно заряженной бесконечной плоскости и равномерно заряженной сферы.
16. Проводники и диэлектрики в электрическом поле. Конденсаторы.
17. Энергия электрического поля. Движение заряженных частиц в электрическом поле.
18. Постоянный ток. Электродвижущая сила (ЭДС). Закон Ома для полной цепи. Правила Кирхгофа.
19. Работа и мощность тока. Закон Джоуля-Ленца.
20. Магнитное поле. Вектор магнитной индукции. Магнитное поле тока.
21. Закон Ампера. Сила Лоренца. ЭДС, индуктируемая в проводнике.
22. Движение заряженных частиц в магнитном поле.
2. Уравнение состояния идеального газа. Внутренняя энергия. Температура.
3. Работа в термодинамике. Циклы. Коэффициент полезного действия (КПД) циклов. Первый закон термодинамики. Теплоемкость. Молярная теплоёмкость.
4. Фазовые переходы. Тепловой баланс.
5. Влажность воздуха. Насыщенный и ненасыщенный пар.
6. Электростатика. Напряженность и потенциал поля равномерно заряженной бесконечной плоскости и равномерно заряженной сферы.
7. Конденсаторы. Постоянный ток. Электродвижущая сила (ЭДС). Закон Ома для полной цепи. Правила Кирхгофа.
8. Закон Джоуля-Ленца. Работа и мощность в электрической цепи.
9. Магнитное поле. Вектор магнитной индукции. Движение заряженных частиц в электромагнитном поле.
10. Закон Ампера. Сила Лоренца.
11. Магнитный поток. Индуктивность. ЭДС, индуктируемая в проводнике. Закон электромагнитной индукции. Правило Ленца.
12. Механические колебания. Математический маятник. Пружинный маятник. Превращения энергии при колебательном движении.
13. Колебательный контур. Превращения энергии при колебательном движении.
14. Геометрическая оптика. Преломление света. Тонкие линзы.
15. Волновая оптика. Интерференция. Дифракция.
16. Механика. Кинематика. Кинематические уравнения для перемещения и для скорости. Равноускоренное движение.
17. Движение тела, брошенного под углом к горизонту. Закон сохранения энергии в кинематических задачах.
18. Динамика. Законы Ньютона.
19. Статика. Момент силы. Условия равновесия твёрдых тел.
20. Элементы квантовой физики.
Олимпиадная физика
2. Средняя скорость.
3. Физические величины. перевод единиц измерения.
4. Задачи на движение различных типов.
5. Графическое решение задач.
6. Длина, площадь, объем.
7. Плотность. Средняя плотность.
8. Силы. Сложение сил.
9. Давление. Гидростатическое давление.
10. Сообщающиеся сосуды и гидравлический пресс.
11. Сила Архимеда. Условие плавания тел.
12. Статика. Условие равновесия рычага.
13. Работа. Мощность. КПД.
14. Законы сохранения.
15. Комбинированные задачи.
I. КИНЕМАТИКА
2. О пользе графиков движения.
3. Геометрия в физике.
4. Относительность движения. Сложение движений и сложение скоростей. Векторы.
5. Переход из одной системы отсчета в другую.
6. Кинематика твердого тела и нерастяжимых нитей.
8. Статика нерастяжимых нитей.
9. Давление. Закон Паскаля в жидкостях и газах.
10. Закон Архимеда. Точка приложения силы Архимеда.
Удельная теплота плавления и парообразования. Уравнение теплового баланса.
12. КПД нагревательных приборов.
13. Теплообмен по закону Ньютона.
15. Электрический ток. Закон Ома. Различные соединения проводников. Удельное сопротивление. Зависимость удельного сопротивления от температуры.
16. Закон Джоуля – Ленца.
17. ЭДС и разность потенциалов.
18. Мостовая схема. Правила Кирхгофа.
19. Бесконечные цепи.
21. Закон отражения света.
22. Закон преломления света. Полное внутреннее отражение.
23. Линзы
Программа нацелена на подготовку школьников к муниципальному и региональному этапам Всероссийской Олимпиады Школьников (ВсОШ)по Физике. Программа рассчитана на дополнительное образование с одной стороны, комплекты заданий ВсОШа работают по принципу накопленного итога и в них не входит тема пройденная накануне этапа ВсОШ с другой стороны, поэтому первая часть нацелена на повторение пройденного материала в 8ом классе и закрепление материала 9ого класса.
1. Скорость, средняя скорость. Решение кинематических задач с помощью графиков.
2. Статика. Условие равновесия. Момент сил, правила моментов.
3. Гидростатическое давление, сообщающиеся сосуды. Сила Архимеда. Изменение уровня жидкостей.
4. Теплота, теплоемкость, фазовые переходы. Уравнение теплового баланса. Закон Ньютона-Рихмана.
5. Электрический ток. Цепи постоянного тока. Понятие потенциала. Последовательное и параллельное соединение. Смешанное соединение, симметрия в цепях.
6. Равноускоренное движение. Уравнения движения. Формула без времени.
7. Движение по окружности. Относительное движение.
8. Криволинейное движение. Полет тела под углом к горизонту.
9.-10. Повторение перед муниципальным туром. Прорешивание заданий прошлых лет.
11. Задачи на поиск минимума и максимума через квадратное уравнение. Повторение.
12. Кинематические связи. Динамика. Законы Ньютона.
13. Динамика систем с кинематическими связями.
14-20. Повторение пунктов 2-7 в контексте решения задач регионального этапа ВсОШ.
21. Закон сохранения импульса. Импульс тела, импульс силы.
22. Теорема об изменении кинетической энергии.
23. Работа сил.
24. Закон сохранения энергии
2. Течение жидкости. Закон Бернулли.
3. Кинематика тела, брошенного под углом к горизонту. Треугольник скоростей.
4. Сила тяготения. Движение небесных тел.
5. Сила трения.
6. Закон сохранения импульса. Понятие центра масс. Теорема о движении центра масс.
7. Молекулярная физика. Закон состояния идеального газа. Работа газа. Первое начало
термодинамики. Малые изменения параметров в газовых задачах.
8. Электростатика. Теорема Гаусса-Остроградского. Теорема единственности. Энергия
взаимодействия зарядов.
9. Приборы с нелинейной ВАХ и расчет схем с их использованием. Черные ящики.
Модели диодов (идеальный, с пороговым напряжением).
10. Конденсаторы.
11. Движение тел с переменной массой.
12. Статика. Принцип виртуальных перемещений.
1. Относительность движения.
2. Кинематические связи в динамике.
3. Движение при наличии сил сухого и вязкого трения.
4. Векторные уравнения в механике.
5. Законы сохранения в механике.
6. Теорема о движении центра масс.
7. Парадокс "большого тела".
8. Движение в гравитационном поле. Законы Кеплера.
9. Неинерциальные системы отсчёта.
10. Принцип Торричелли.
11. Экстремальные задачи механики.
II. Избранные вопросы термодинамики
1. Анализ графических зависимостей.
2. Полунепроницаемые перегородки.
3. Первое начало термодинамики.
4. Теплоёмкость газа. Политропический процесс.
5. Тепловые двигатели. Холодильные машины.
6. Насыщенный пар. Влажный воздух.
III. Электродинамика
1. Заряженные плоскости и заряженные сферы.
2. Теорема единственности в электростатике.
3. Правила Кирхгофа.
4. Метод узлового потенциала.
5. Методы расчёта эквивалентных элементов.
6. Анализ цепей, находящихся в "чёрном ящике".
7. Цепи с нелинейными элементами.
8. Цепи с конденсаторами.
9. Электрический ток в различных средах.
10. Движение заряженных частиц в электрическом и магнитном поле.
11. Электромагнитная индукция. Индуктивность.
IV. Механические и электромагнитные колебания
1. Колебания простейших механических систем.
2. Кинематика колебательного движения.
3. Колебания жидкости.
4. Колебания сложных механических систем.
5. Колебательный контур.
6. Цепи переменного тока с нелинейными элементами.
V. Геометрическая оптика
1. Плоское зеркало.
2. Тонкая линза.
3. Сферическое зеркало.
4. Оптические системы.
VI. Общие методы решения олимпиадных задач
1. Метод размерности.
2. Метод аналогий.
3. Метод подобия.
4. Метод обратимости.
5. Графические методы.
6. Метод дифференцирования и интегрирования.
7. Оценочный метод.
Кроме того, занятия предшествующие дням проведения этапов Всероссийской олимпиады и
олимпиады МФТИ будут полностью посвящены разбору особенностей этих олимпиад на примере
задач последних лет.
Компьютерная физика
№
Тематический план занятий по компьютерной физике
Основы создания программных моделей (10 часов)
1.
2
Аналоговый и цифровой миры. Алгоритм. Программные модели.
2.
2
Основные библиотеки и команды языка PYTHON.
3.
2
ЛР*. Измерение малых величин. Калибровка цифрового секундомера
4.
2
Графические модули PYTHON. Отображение сложных фигур
5.
2
ЛР Измерение площади фигуры неправильной формы. Погрешности
Кинематика и динамика (10 часов)
6.
2
Механическое движение. Траектория. Путь
7.
2
Прямолинейное равномерное движение. Скорость.
8.
2
ЛР. Измерение скорости движения шарика по наклонной плоскости
9.
2
Плотность вещества. Связь массы, плотности и объема
10.
2
ЛР. Определение плотности композитного материала
Строение и свойства вещества (10 часов)
11.
2
Строение вещества. Строение атома. Квантовая физика.
12.
2
Свойства газов. Диффузия газов.
13.
2
Наночастицы и их уникальные свойства
14.
2
Свойства жидкостей. Закон Архимеда
15.
2
Давление. Гидравлический пресс
Закон сохранения механической энергии (8 часов)
16.
2
Работа. Мощность. Полезная работа. КПД.
17.
2
Простые механизмы. Рычаг. Блок.
18.
2
Потенциальная энергия. Кинетическая энергия.
19.
2
Сила упругости. Деформация тела. Закон Гука.
20.
2
Дипломный проект. Определение длины и веса рулонных материалов
40
Всего часов

8. Измерение скорости движения шарика на экране
№
Тематический план занятий по компьютерной физике
Основы создания программных моделей (10 часов)
1.
2
Аналогово – цифровое преобразование. Программные модели.
2.
2
Основные библиотеки и команды языка PYTHON.
3.
2
ЛР*. Измерение малых величин. Калибровка цифрового секундомера
4.
2
Аппроксимация физических объектов. Погрешности
5.
2
ЛР Измерение площади фигуры неправильной формы
Кинематика (8 часов)
6.
2
Прямолинейное равномерное движение
7.
2
ЛР. измерение скорости движения шарика по наклонной плоскости.
8.
2
Равноускоренное движение
9.
2
Движение по окружности. Центростремительное ускорение
Основы молекулярной физики (8 часов)
10.
2
Строение вещества. Строение атома. Квантовая физика.
11.
2
Наночастицы и их уникальные свойства.
12.
2
Тепловое движение. температура и её измерение
13.
2
ЛР. Сравнение количеств теплоты при смешивании воды разной Tº
Основы электродинамики (8 часов)
14.
2
Электризация тел, электрический заряд, виды зарядов.
15.
2
Закон Ома для участка цепи.Схемы электрических цепей.
16.
2
ЛР. Регулирование силы тока реостатом.
17.
2
Опыт Эрстеда. Магнитное поле, магнитная энергия.
Оптика (6 часов)
18.
2
Законы отражения и преломления света.
19.
2
ЛР. Изучение законов отражения света. Световая ловушка.
20.
2
Дипломный проект. Определение длины и веса рулонных материалов.
40
Всего часов


8. Измерение скорости движения шарика на экране

Русский язык
1
Входная контрольная работа. Правописание безударных гласных в корне. Тире между подлежащим и сказуемым.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
1
Входная контрольная работа. Правописание безударных гласных в корне. Тире между подлежащим и сказуемым.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Контрольная работа в формате ЕГЭ.
28
Информатика
![]()

Анохина Дарья Сергеевна
Педагог 1-й квалификационной категории.
Член экзаменационной комиссии по сертификации педагогических работников в рамках проекта IT-вертикаль/ИТ класс в московской школе, член рабочей группы по разработке оценочных средств ГАОУ ДПО «Корпоративный университет».
Преподаватель подготовительных курсов МФТИ.
№ занятия
Тема
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
№ занятия
Тема
1
2
3
4
5
6
Перебор слов и системы счисления.
7
Работа с таблицами (Excel).
8
9
Вычисление количества информации.
10
11
12
13
14
Рекурсивные алгоритмы.
15
16
17
Выигрышная стратегия (Задание 1)
18
Выигрышная стратегия (Задание 1)
19
Выигрышная стратегия (Задание 1)
20
21
Выигрышная стратегия (Задание 2)
22
Выигрышная стратегия (Задание 2)
23
Выигрышная стратегия (Задание 2)
24
Выигрышная стратегия (Задание 3)
25
Выигрышная стратегия (Задание 3)
26
Выигрышная стратегия (Задание 3)
27
28
Анализ программ с циклами и условным оператором.
29
Оператор присваивания и ветвления. Перебор вариантов, построение дерева.
30
Обработка символьных строк.
31
Обработка целочисленной информации.
32
Программирование. Работа с файлами.
33
Программирование. Работа с файлами.
34
Программирование. Работа с файлами.
35
Программирование. Работа с файлами.
36
№ занятия
Тема
1
Решение тестового КИМа.
2
Разбор функций с применением правил логических выражений и построениетаблиц.
3
Анализ программ (чтение кода и понимание принципов его работы).
4
Исполнители на плоскости. Арифмометры. Посимвольное десятичное преобразование. Передача информации. Передача файлов. Сравнение нескольких способов передачи. Определить размер файла.
5
6
Перебор слов и системы счисления.
7
Работа с таблицами (Excel).
8
Работа с таблицами (Excel). Поиск символов в текстовом редакторе.
9
Вычисление количества информации.
10
11
Исполнители Редактор, Чертёжник, условные операторы.
12
Кодирование чисел. Системы счисления.
13
Множества. Числовые отрезки. Координатная плоскость. Побитовая конъюнкция.
14
Рекурсивные алгоритмы.
15
Срез. Проверочная работа на основе полученных данных. Анализ ошибок.
16
Робот-сборщик.
17
Выигрышная стратегия (Задание 1)
18
Выигрышная стратегия (Задание 1)
19
Выигрышная стратегия (Задание 1)
20
Срез. Проверочная работа на основе полученных данных.Анализ ошибок.
21
Выигрышная стратегия (Задание 2)
22
Выигрышная стратегия (Задание 2)
23
Решение тестового КИМа.
24
Выигрышная стратегия (Задание 3)
25
Выигрышная стратегия (Задание 3)
26
Выигрышная стратегия (Задание 3)
27
Проведение пробного ЕГЭ.
28
Анализ программ с циклами и условным оператором.
29
Оператор присваивания и ветвления. Перебор вариантов, построение дерева.
30
Обработка символьных строк.
31
Обработка целочисленной информации.
32
Проведение пробного ЕГЭ.
33
Программирование. Работа с файлами.
34
Программирование. Работа с файлами.
35
Программирование. Работа с файлами.
36
Срез. Проверочная работа на основе полученных данных.Анализ ошибок.
Программирование
- Создавать нового пользователя (id, password)
- Изменять пароль у выбранного пользователя
- Выводить на экран всех пользователей (id’s)
- Выход из приложения
- Курс обеспечен методическими материалами и домашними заданиями, выполняя которые, помимо укрепления знаний, полученных на занятии, ребята смогут копить баллы за каждое выполненное задание! Также баллы отображают уровень прогресса в обучении.
- Все материалы и задания доступны на платформе дистанционного обучения Google Classroom, что в совокупности с использованием Google Colaboratory для изучения Python, делает возможным обучение с любого компьютера, подключенного к сети Интернет
- Никаких дополнительных установок программного обеспечения для Python не требуется.
- Существенным достоинством данного курса является организация самостоятельной работы школьников в форме домашних заданий.
1. Программирование 7 класс, базовый уровень
Программирование 7 класс, базовый уровень.
Преподаватель курса Лантратов Артем Андреевич
Образование КГУ, Краснодар.
Факультет математики и компьютерных наук. Бакалавр.
Преподаватель информатики, математики,программирования (PYTHON 3 , VBA, C#), курсов по вебу (HTML 5+CSS3).
Разработчик Python (разработка телеграм ботов, парсеров (Beautiful Soup 4, Selenium, requests, pandas,Tkinter).
Программирование на Python 3(написание парсеров с использованием библиотек: bs 4, selenium, pandas,Tkinter;
боты для телеграмм (pytelegrambot), работа с Flask, Django)
Разработка Игр (Scratch, Pencil Code, Construct 3, Unity)
Опыт работы с *nix системами
Преподаватель подготовительных курсов «Физтех-Потенциал».
Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование.
Тестирование высылается после регистрации. Выполняется в письменном виде и отправляется на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
| № занятия | Тема |
| 1 |
Знакомство с Python. Ввод и вывод данных с помощью функций input() и print(). Переменные и типы данных. Операции с числами. |
| 2 |
Знакомство с Python. Операции сравнения. Логические операции. Условная конструкция if. |
| 3 |
Строки. Операции со строками. Методы форматирования строк. |
| 4 |
Циклы. Работа с циклами while и for. Функция range(). Модуль random. |
| 5 |
Структуры данных. Списки, словари и множества. |
| 6 |
Модуль Turtle. Наглядное применение полученных знаний с помощью рисования геометрических фигур. |
| 7 |
Модуль Turtle. Работа со сложными геометрическими фигурами. |
| 8 |
Функциональное программирование. Введение в функции. Функции с определённым и неопределённым количеством параметров. Область видимости переменных. |
| 9 |
Игровое программирование. Создание игры камень, ножницы, бумага. Создание игры кубики яцзы. |
| 10 |
Игровое программирование. Создание игры Smiley Pong. |
| 11 |
Игровое программирование. Создание программы Шифр Цезаря. Создание игры крестики-нолики. |
| 12 |
Игровое программирование. Создание игры “Охотник за сокровищами”. |
| 13 | Решение задач. |
| 14 |
Работа с файлами. Функции read(), readln(), write(), writeln(). Контекстный менеджер with. |
| 15 |
Создание графического интерфейса. Работа с виджетами и их положением относительно осей x и y. |
| 16 |
Создание программ с графическим интерфейсом. Создание приложения “Генератор случайных паролей”. |
| 17 |
Создание программ с графическим интерфейсом. Работа с данными, которые будут нам отдавать другие приложения (API). Создание приложения “Погода”. |
| 18 |
Создание программ с графическим интерфейсом. Создание приложения “Калькулятор”. Работа с сеткой приложения. |
| 19 |
Объектно-ориентированное программирование. Классы и объекты. |
| 20 |
Объектно-ориентированное программирование. Классы и объекты. |
| 21 |
Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Инкапсуляция”. |
| 22 |
Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Наследование”. |
| 23 |
Объектно-ориентированное программирование. Изучение парадигмы ООП под названием “Полиморфизм”. |
| 24 |
Объектно-ориентированное программирование. Изучение класса object. Строковое представление объекта. |
| 25 |
Объектно-ориентированное программирование. Создание приложения для регистрации пользователя. Приложение будет уметь: |
| 26 |
Объектно-ориентированное программирование. Создание игры “Властелин разума”. |
| 27 |
Парсинг данных. BeautifulSoup. Сбор простых данных с сайтов. |
| 28 |
Парсинг данных. BeautifulSoup. Сбор табличных данных с сайтов. |
| 29 |
Парсинг данных. BeautifulSoup. Сбор данных с многостраничных сайтов. |
| 30 |
Парсинг данных. BeautifulSoup. Применение продвинутых техник при сборе данных. |
| 31 |
Парсинг данных. BeautifulSoup. Сбор данных с сайтов с подгружаемой информацией (данные подгружаются с помощью JavaScript). |
| 32 |
Парсинг данных. Selenium. Сбор данных с помощью эмуляции работы пользователя. |
| 33 |
Парсинг данных. Selenium + BeautifulSoup. Комбинируем две библиотеки для оптимизации процесса сбора данных. |
| 34 | Выбор итогового проекта и начало работы над ним. |
| 35 | Работа над итоговых проектом. |
| 36 | Презентация и защита итоговых проектов. |
Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование.
2. Программирование 7 класс, продвинутый уровень
Курс рассчитан на более глубокое погружение в сам язык программирования. Будем изучать продвинутые функции, понимать, как они работают и писать свои версии этих функций (алгоритмы).
Будем решать много разноплановых задач, с помощью которых подготовимся к участию в олимпиадах по программированию.
Программа курса будет размещена в ближайшее время. Следите за обновлением информации
Для распределения в группы базового и профильного уровней необходимо будет пройти тестирование.
Тестирование высылается после регистрации. Выполняется в письменном виде и отправляется на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
3. Анализ данных на Python. Профильное программирование (10-11 класс)
Автор и преподаватель курса Лазарева Светлана Александровна.
Доцент кафедры информатики и вычислительного эксперимента Института математики, механики и компьютерных наук Южного федерального университета (ЮФУ),
кандидат технических наук.
Доцент по специальности 05.13.11 «Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей».
«Анализ данных на Python» – годовой курс (36 занятий по 4 ак.ч. в неделю), направленный на изучение и практическое использование Python-библиотек для работы с данными, на разработку моделей машинного обучения.
В последнем разделе курса ученики познакомятся с технологическим процессом коллективной разработки программного обеспечения, а первый раздел курса — повторение основ Python — будет хорошей базой для тех, кто решит использовать этот язык при сдаче ЕГЭ по информатике. Все разделы курса указаны в учебном плане.
Зачисление на курс «Анализ данных на Python» проходит по результатам входного теста (тест высылается после регистрации).
Программа курса
| № | Тема | Краткое содержание |
| Раздел 1. Основы Python | ||
| 1 | Вводное занятие | Знакомство. Обзор курса. Язык Python. Интерпретатор Python. Использование локальных и удаленных сред для разработки программ на Python. Среда дистанционного обучения Google Classroom и Google Colaboratory. |
| 2 | Типы данных. Операторы. | Закрепление и повторение тем. Основные типы. Операторы. Специфика изменяемых и неизменяемых типов. Циклы. Break, continue. Вложенные циклы. |
| 3 | Функции и файлы | Тест 1. Закрепление темы "Функции и файлы". Решение задач по теме "Функции". Написание программ обработки файлов. |
| 4 | Модули | Создание модуля. Подключение модуля. Импортирование. Использование псевдонимов. Область видимости переменных модуля. Решение задач. |
| 5 | Элементы функционального программирования | Лямбда-выражения. Функция как объект. Генератор списка. Функции map, filter, reduce. Декораторы. |
| 6 | ООП-1 | Встроенные объекты. Методы и свойства. Классы. Построение собственных классов. Экземпляры. Наследование. |
| 7 | ООП-2 | Служебные методы. Переопределение операций. "Утиная" типизация. Иерархия классов. |
| 8 | ООП-3 | Интерфейсы. Распространенные шаблоны поведения объектов. Итераторы и генераторы. Исключения. Иерархия исключений. |
| 9 | Ключевая точка-1 (Основы Python) | Ключевая точка-1. Опрос мнений |
| Раздел 2. Введение в анализ данных | ||
| 10 | Введение в анализ данных. Введение в математическую статистику | Мат. статистика, основные понятия: выборка данных, среднее, медиана, дисперсия. Понятие "выброс". Виды распределения данных. Корреляция. Примеры использования. Классические задачи машинного обучения. |
| 11 | Основы pandas, занятие 1 | Обзор библиотек Python для работы с данными. Структуры данных pandas. Базовая функциональность. Выборка и фильтрация. |
| 12 | Основы pandas, занятие 2 | Переформатирование данных: очистка, преобразование. Обработка отсутствующих данных. Преобразование данных: изменение типов, замена значений. |
| 13 | Основы pandas, занятие 3 | Уникальные значения. Удаление дубликатов. Группировки. Решение задач. |
| 14 | Основы Pandas, занятие 4. | Слияние данных. Описательные статистики. Выбросы. Решение задач по теме. |
| Раздел 3. Визуализация данных | ||
| 15 | Визуализация данных: matplotlib, занятие 1 | Массивы в numpy. Рисунки и графики. Цвет, маркер, линия. Метки и надписи. Сохранение графика в файле. |
| 16 | Визуализация данных: matplotlib, занятие 2 | Функции построения графиков. Линейные графики. Диаграммы. Гистограммы. |
| 17 | Визуализация данных: matplotlib, занятие 3 | Создание анимированных графиков. Модуль matplotlib.animation. Класс FuncAnimation. Сохранение анимации. Создание трёхмерных анимаций. |
| 18 | Визуализация данных: matplotlib, занятие 4 | Применение matplotlib для визуализации структур данных pandas. Нанесение данных поверх изображения. Решение задач. |
| 19 | Ключевая точка-2 (Pandas и matplotlib). |
Ключевая точка-2. |
| Раздел 4. NumPy и введение в машинное обучение | ||
| 20 | Основы NumPy, занятие 1 | Быстродействие NumPy. Основные понятия. Вектор. Массив. Многомерный массив. Операции массив-скаляр. Индексирование. Вырезание. Транспонирование. |
| 21 | Основы NumPy, занятие 2 | Обработка данных с применением массивов. Сортировки. Теоретико-множественные операции. Устранение дубликатов. |
| 22 | Основы NumPy, занятие 3. | Файловый ввод-вывод массивов. Двоичный и текстовый формат. Модуль math. Константы. Округление чисел. Тригонометрические функции. Дробная и целая части чисел. Квадратный корень. Преобразование градусов в радианы. Решение задач. |
| 23 | Основы NumPy, занятие 4. | Понятие математической модели. Аналитические и численные решения. Аппроксимация функции многочленом. Перевод категориальных признаков в числовые. Решение задач. |
| 24 | Применение изученных библиотек для решения задач машинного обучения | Понятия точности, погрешности. Примеры решения базовых задач МО. Этапы обработки и анализа данных. Особенности применения изученных библиотек при работе с "сырыми" данными. Kaggle - площадка датасетов, соревнований по машинному обучению и визуализации. |
| 25 | Введение в машинное обучение. Библиотека scikit-learn, занятие -1 | Что такое машинное обучение (machine learning, ML)? Постановка задачи. Понятие модели. Входные признаки. Целевая переменная. Репрезентативность обучающей выборки. Понятие метрики качества. Обучение с учителем и без. Знакомство со встроенными наборами данных scikit-learn. Нормализация данных. Визуализация данных. |
| 26 | Библиотека scikit-learn, занятие -2 | Разделение данных на множества: тренировочное и тестовое. Генерация прогнозов. Линейная регрессия. Обучение линейной регрессии. Понятие переобучения. |
| 27 | Библиотека scikit-learn, занятие -3 | Рекомендательные системы. Использование метрик и корреляции для построения рекомендательных систем. |
| 28 | Библиотека scikit-learn, занятие -4 | Кластеризация с помощью графовых методов. Кластеризация методом Forel. |
| 29 | Библиотека scikit-learn, занятие -5 | Кластеризация методом K-means. |
| 30 | Ключевая точка - 3 (numpy и scikit-learn). | Ключевая точка - 3 (numpy и scikit-learn). |
| Раздел 5. Работа над проектами | ||
| 31 | Работа над проектами | Структура проекта. Разработка архитектуры приложения. Согласование интерфейсов. Классификатор. Обучение классификаторов. Метод k-ближайших соседей. |
| 32 | Основы проектной работы. Git, GitHub | Связь с Google Disk и GitHub. Настройки совместного использования файлов. Возможности документирования кода. Дополнительные библиотеки и вычислительные ресурсы. Технология работы над проектами. Открытые и закрытые репозитории. Понятие "контроль версий". Веб-хостинг проектов с поддержкой системы контроля версий. |
| 33 | Основы проектной работы. Git, GitHub | Создание собственного репозитория. Ветвление. Копирование на локальную машину. Перенос изменений в главный репозиторий. |
| 34 | Работа над проектами | Создание репозитория проекта. Работа над кодом. |
| 35 | Тестирование приложений. | |
| 36 | Защита проектов |
Учебные занятия по курсу проходят в дистанционном формате на платформе Zoom.
ü Домашние задания доступны сразу после занятия.
ü Домашнее задание не только проверяется на правильность результата, но и подробно разбирается с точки зрения стиля программирования и эффективности решения.
ü Ко всем заданиям доступны презентации с материалами занятий и рекомендованные ссылки на интернет-ресурсы, полезные для закрепления темы.
ü При возникновении трудностей можно связаться с преподавателем.
ü Благодаря использованию Google Classroom, учащиеся всегда имеют возможность обсудить интересующие их вопросы в ленте курса, получить напоминание о дате сдачи домашнего задания, посмотреть накопленные баллы и т.д.
4. Программирование логических игр и головоломок и начала компьютерного моделирования
(8-10 классы)
Курс представляет собой введение в программирование для начинающих на основе разработки компьютерных игр и головоломок в текстовом (консольном) режиме, с последующим переходом к основам компьютерного моделирования процессов разной природы (физических, технических, биологических и экономических).
Зачисление по результатам тестирования.
Принципиальная особенность и новизна курса – работа учащихся над кодом игры \ головоломки на двух языках программирования: сначала вместе с преподавателем разбирается (готовый) код на языке Basic, потом производится работа (самостоятельная и под руководством преподавателя) по переводу этого кода на Python.
В качестве первого языка разработки предполагается использование Basic, это принципиальный и осознанный выбор. Язык Basic идеально подходит для учебных целей, именно на нем исторически накоплена наиболее богатая библиотека занимательных головоломок и логических игр, причем большая часть этого материала до сих пор не переведена на другие языки. Именно такой материал позволяет заложить основу четкого алгоритмического мышления, необходимого при профессиональном освоении любых «взрослых» (промышленных) языков программирования.
Помимо освоения основ обоих языков, такая философия курса способствует качественно более глубокому и объемному усвоению и пониманию используемых алгоритмов. Учащиеся учатся понимать, что логика программы и того или иного алгоритма не привязана к конкретному языку; тем не менее и одновременно, производится проработка базовых конструкций конкретных языков.
Практика показала чрезвычайную педагогическую эффективность такой методики «перевода» сложных алгоритмов с одного языка на другой.
Программа курса:
Занятия 1-2. Основы языка программирования Basic. Построение и отрисовка лабиринта.
Занятия 3-5. Основы языка Basic (продолжение). Игра Авари.
Занятия 6-8. Игра «Виселица».
Занятия 9-11. Игра «Быки и коровы» (MasterMind) – упрощенная версия. Основы языка программирования Python.
Занятия 12-13. Карточная игра Acey-Ducey.
Занятия 14-16. Игра «Найти льва в пустыне».
Занятия 17-19. Игра «Колышковый солитер»
Занятия 20-22. Игра «Жизнь».
Занятия 23-25. Игра «Жизнь» для двоих.
Занятия 26-30. Игра «Король» (управление территорией).
Более точное содержание занятий может варьироваться в зависимости от уровня учащихся в набранной группе. В частности, может меняться перечень игр. Кроме подробно разбираемых на занятиях игр, слушатели курса получают, после его окончания, много листингов других игр для самостоятельной проработки дома.
Технически, на занятиях предполагается использование современных (учебных) онлайн-компиляторов, от учащихся требуется только наличие домашнего компьютера (десктоп или ноутбук) и доступ к Интернет
5. «Решение задач повышенной сложности на разных языках (Python\JavaScript)» (8-10 классы)
Курс представляет собой коллекцию вычислительных задач повышенной сложности (с постепенным повышением этой сложности), отобранных из разных источников, и предполагает их разбор на нескольких языках программирования. Сначала происходит разбор решения задачи на одном языке, потом разобранный алгоритм переносится на другой язык.
Смысл этого подхода состоит не только в том, чтобы показать учащимся возможности разных языков в их сравнении (что само по себе одна из задач курса), но также в том, чтобы приучить школьников к основам грамотной философии программирования: алгоритм решений той или иной задачи существует сам по себе, независимо от его имплементации (реализации) на каком-то языке, и возможны многочисленные такие имплементации.
Необходимо тестирование.
Задачи для курса выбраны из следующих источников:
(1) Задачи по программированию олимпиад технических ВУЗ-ов для школьников советских лет.
(2) Книга Michael Wiesenberg «Puzzled programmer: 15 mind-boggling puzzles to test your progrаmming prowess» («15 поражающих воображение загадок чтобы проверить ваше искусство программиста»), Microsoft Press, 1987.
Задачи составлены таким образом, что для их эффективного решения (иногда – просто хоть какого-то решения) практически невозможно придумать очевидный алгоритм, решающий задачу «в лоб»: требуется предварительный анализ математической структуры задачи. При этом, решить задачу чисто аналитически, тоже невозможно. Таким образом, предложенные задачи принадлежат к нетривиальному типу: их можно решить только совместным использованием аналитического подхода и компьютерного перебора вариантов.
(3) Задачи из проекта "Эйлер". Проект Эйлер — это набор интригующих задач по математике и программированию, для решения которых, однако, недостаточно одной только математической интуиции. Разумеется, математика поможет прийти к красивому и элегантному решению, но для успешного решения большинства задач без навыков программирования не обойтись.
Примеры разбираемых задач из книги “Puzzled programmer: 15 mind-boggling puzzles”:
1. Найти все ряды последовательных целых чисел, сумма которых равна ровно 10000.
2. Используя все цифры от 1 до 9, составить три трехзначных числа с максимальным произведением и минимальным произведением.
3. Найти два рациональных числа, сумма кубов которых равна 6.
4. Найти шестизначное число такое что, если его разбить на два трехзначных числа, сложить эти числа и возвести в квадрат, получится исходное число.
5. Найти 4-значное число, которое равно сумме четвертых степеней своих цифр.
6. Найти наименьшее число, которое можно представить в виде суммы двух кубов натуральных чисел двумя разными способами.
7. Найти первые пять рядов последовательных целых чисел таких что каждую такую последовательность можно разбить на две группы и в сумма квадратов чисел в первой группе равна сумме квадратов чисел во второй группе. Первая такая последовательность хорошо известна: 3^2 + 4^2 = 5^2. Считать известным, что в каждой такой последовательности нечетное количество всех чисел, а в правой стороне равенства присутствует на одно больше число, чем в правой.
8. Найти четыре различных числа, которые как при сложении, так и умножении дают один результат, равный 9.81.
Примеры разбираемых задач из проекта «Эйлер»:
1. Если выписать все натуральные числа меньше 10, кратные 3 или 5, то получим 3, 5, 6 и 9. Сумма этих чисел равна 23. Найдите сумму всех чисел меньше 1000, кратных 3 или 5.
2. Каждый следующий элемент ряда Фибоначчи получается при сложении двух предыдущих. Начиная с 1 и 2, первые 10 элементов будут: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Найдите сумму всех четных элементов ряда Фибоначчи, которые не превышают четыре миллиона.
3. Простые делители числа 13195 - это 5, 7, 13 и 29. Каков самый большой делитель числа 600851475143, являющийся простым числом?
Технически, предполагается использование современных (учебных) онлайн-компиляторов, от учащихся требуется только наличие домашнего компьютера (десктоп или ноутбук) и доступ к Интернет. Требуется владение Python или JavaScript начального уровня.
Техническое требование для онлайн обучения: работающий микрофон, либо гарнитура. Необходимо проверять исправность до начала занятий.
Занятия проводят квалифицированные преподаватели МФТИ и лучшие учителя московских школ, обладающие большим педагогическим опытом и эффективными методиками подготовки к экзаменам.
Статистика
Расписание курсов
Расписание ОЧНЫХ годовых курсов 2023/2024 Долгопрудный Следите за обновлением информации Следите за обновлением информации ![]()
ОЧНЫЕ ЗАНЯТИЯ 2023/2024 (7-11 классы) МФТИ, г. Долгопрудный
день недели
класс
1
2
3
понедельник
7 класс
8 класс
9 класс
10 класс
11 класс
вторник
7 класс
8 класс
9 класс
10 класс
11 класс
среда
7 класс
8 класс
9 класс
10 класс
11 класс
четверг
7 класс
8 класс
9 класс
10 класс
11 класс
пятница
7 класс
8 класс
9 класс
10 класс
11 класс
суббота
7 класс
8 класс
9 класс
10 класс
11 класс
воскресенье
7 класс
Компьютерная физика
12.15-14.15
Джумаев М.Р. Школьный курс "Экспериментальная физика"
9.00-11.00
Куракин П.В.
Школа №1
(начало занятий
с октября)
8 класс
Компьютерная физика
12.15-14.15
Джумаев М.Р.Школьный курс "Экспериментальная физика"
11.30-14.00
Куракин П.В.
Школа №1
(начало занятий
с октября)
9 класс
10 класс
Профильная математика
10.00-13.00
Колымагина Е.А.
Школа №1
11 класс
Математика
(Подготовка к ЕГЭ)
13.30-16.30
Колымагина Е.А.
Школа №1
Расписание ОЧНЫХ годовых курсов 2023-2024 класс, в который перешел ученик Информатика ОГЭОЧНЫЕ ЗАНЯТИЯ 2023-2024 (7-11 классы) Московский корпус МФТИ, г. Москва
день недели
класс
1
2
3
4
понедельник
7 класс
8 класс
9 класс
Профильная математика
(Подготовка к ОГЭ)
17.15-20.15
Софронова А.А.
10 класс
11 класс
вторник
7 класс
8 класс
Олимпиадная физика
17.00-19.30
Шишов Е.А.
9 класс
10 класс
Профильная физика
17.00-20.00
Прохоров В.К.
11 класс
Экспресс-курс ЕГЭ от Физтеха
(математика)
17.00-20.00
Николаев Ю.П. Математика.
Подготовка к заключительному этапу перечневых олимпиад
I уровня 2024
17.00-20.00
Николаев Ю.П.
среда
7 класс
8 класс
9 класс
Школьный курс
"Экспериментальная физика"
Ершова Л.В.
17.00-20.00
(начало занятий с октября)
10 класс
Профильная математика
17.00-20.00
Банарь А.А.
11 класс
Профильная физика
(подготовка к ЕГЭ )
17.00-20.00
Киркинский А.И.
четверг
7 класс
Школьный курс "Экспериментальная
физика"
17.00-19.00
Шишов Е.А.
(начало занятий с октября)
8 класс
9 класс
Тематический курс по физике "Молекулярная физика и термодинамика"
17.00-20.00
Киркинский А.И.
(январь - февраль)
10 класс
Тематический курс по физике "Молекулярная физика и термодинамика"
17.00-20.00
Киркинский А.И.
(январь - февраль)
11 класс
Тематический курс по физике "Молекулярная физика и термодинамика"
17.00-20.00
Киркинский А.И.
(январь - февраль)
пятница
7 класс
8 класс
9 класс
10 класс
11 класс
суббота
7 класс
Профильная математика Огнева Е.Г.
12.45 14.45 Олимпиадная математика
10.00-12.00
Кисловская В.Д.
8 класс
Профильная математика
10.00-12.30
Огнева Е.Г. Олимпиадная математика
10.00-12.30
Ивонцин Л.А. Профильная физика
12.45-15.15
Ивонцин Л.А.
9 класс
13.00-16.00
Анохина Д.С.Профильная физика
Подготовка к ОГЭ
17.00-20.00
Юдин И.С.
2 группа
(начало занятий
с октября)
10 класс
11 класс
Профильная математика (ЕГЭ)
Банарь А.А.
13.00-16.00
1 группа Профильная математика (ЕГЭ)
Банарь А.А.
16.00-19.00
2 группа
(начало занятий
с октября)
воскресенье
7 класс
Профильная физика
13.30-15.30
Ершова Л.В.
Программирование Python.
Базовый уровень.
10.00-12.00
Лантратов А.А.
8 класс
9 класс
Профильная физика
(Подготовка ОГЭ)
10.00-13.00
Ершова Л.В.
Набор закрыт
10 класс
Информатика Python.
Базовый уровень
12.30-15.30
Лантратов А.А. Информатика Python.
Профильный уровень
16.00-19.00
Лантратов А.А.
(Входное тестирование)
11 класс
Информатика Python.
Базовый уровень
12.30-15.30
Лантратов А.А. Информатика Python.
Профильный уровень
16.00-19.00
Лантратов А.А.
(Входное тестирование)
Информация на согласовании Расписание годовых курсов онлайн 2023-2024 класс, в который перешел ученик
ОНЛАЙН ЗАНЯТИЯ 2023-2024 (7-11 классы)
день недели
класс
1
2
3
4
понедельник
7 класс
Профильная физика
16.30-18.30
Ершова Л.В. Олимпиадная физика
18.40-20.40
Ершова Л.В.
8 класс
Экспериментальная физика
17.00-19.30
Шишов Е.А.
(с октября)
9 класс
Олимпиадная физика
18.00-21.00
Порядин А.И.
10 класс
Математика.
Подготовка к заключительному этапу перечневых олимпиад
I уровня 2024
19.30-21.00
Агаханова Я.С.
(занятия 2 раза в неделю до конца апреля)
Набор закрыт
11 класс
Экспресс-курс ЕГЭ от Физтеха
(физика)
17.00-20.00
Прохоров В.К.
(с 1 марта)
вторник
7 класс
Программирование
Pyton. База
17.00-19.00
Анохина Д.С.
2 группа
8 класс
Профильная физика
17.00-19.30
Ершова Л.В.
«Решение задач повышенной сложности на разных языках
(Python\JavaScript)»
17.00-20.00
Куракин П.В.
(с октября)
9 класс
Профильная математика
(Подготовка к ОГЭ)
17.00-20.00
Порядин А.И.
2 группа
(с октября)Профильная физика
(Подготовка к ОГЭ)
17.30-20.30
Бондарова О.И.
Набор закрыт
«Решение задач повышенной сложности на разных языках
(Python\JavaScript)»
17.00-20.00
Куракин П.В.
(с октября)
10 класс
Физика.
Подготовка к заключительному этапу перечневых олимпиад
I уровня 2024
18.00-21.00
Бондаров М.Н.
(занятия до конца апреля)
Набор закрыт
«Решение задач повышенной сложности на разных языках
(Python\JavaScript)»
17.00-20.00
Куракин П.В.
(с октября)
11 класс
Профильная математика
(Подготовка к ЕГЭ)
19.30-21.00 Агаханова Я.С.
(занятия 2 раза в неделю)
Набор закрыт
среда
7 класс
Программирование Python.
Профильный уровень
17.00-19.00
Анохина Д.С.
2 группаКомпьютерная физика
18.00-20.00
Джумаев М.Р. Программирование Python. Базовый уровень
18.00-20.00
Лантратов А.А.
8 класс
Профильная математика
17.00-19.30
Огнева Е.Г.
Компьютерная физика
18.00-20.00
Джумаев М.Р.
9 класс
Профильная физика
17.00-20.00
Прохоров В.К.
2 группа
(с октября)
Экспериментальная физика
17.00-20.00
Ершова Л.В.
(с октября)Программирование "Анализ данных на Python. Профильный уровень"
17.00-20.00
Лазарева С.А.
(входное тестирование)
10 класс
Математика.
Подготовка к заключительному этапу перечневых олимпиад
I уровня 2024
19.30-21.00
Агаханова Я.С.
(занятия 2 раза в неделю)
Набор закрыт
Информатика Python. Базовый уровень
18.00-21.00
Попов В.С. Программирование "Анализ данных на Python. Профильный уровень"
17.00-20.00
Лазарева С.А.
(входное тестирование)
11 класс
Информатика Python. Базовый уровень
18.00-21.00
Попов В.С.Программирование "Анализ данных на Python. Профильный уровень"
17.00-20.00
Лазарева С.А.
(входное тестирование)
четверг
7 класс
Профильная математика
17.00-19.00
Огнева Е.Г.
8 класс
Информатика
(новый курс)
17.00-19.30
Анохина Д.С.
9 класс
Профильная математика
17.00-20.00
Порядин А.И.
Набор закрыт
10 класс
Информатика Python.
Профильный уровень
18.00-21.00
Попов В.С.
11 класс
Профильная математика
(Подготовка к ЕГЭ)
19.30-21.00
Агаханова Я.С.
(занятия 2 раза в неделю)
Набор закрытИнформатика Python. Профильный уровень
18.00-21.00
Попов В.С. Профильная физика
17.00-20.00
Прохоров В.К.
2 группа
(с ноября)
пятница
7 класс
Экспериментальная физика
17.00-19.00
Шишов Е.А.
(с октября)
8 класс
Программирование логических игр и головоломок и начала компьютерного моделирования
17.00-20.00
Куракин П.В.
(с октября)
9 класс
Олимпиадная математика
18.00-21.00
Порядин А.И.
Программирование логических игр и головоломок и начала компьютерного моделирования
17.00-20.00
Куракин П.В.
(с октября)
10 класс
Профильная физика
18.30-21.30
Асеев Е.М.
Набор закрыт
Экспресс-курс.
Профильная физика
17.00-20.00
Корнеев В.Т.
(январь) Программирование логических игр и головоломок и начала компьютерного моделирования
17.00-20.00
Куракин П.В.
(с октября)
11 класс
Экспресс-курс ЕГЭ от Физтеха
(математика)
17.00-20.00
Николаев Ю.П.
(с 1 марта)
суббота
7 класс
"Геометрия - это просто!" (Планиметрия)
17.30-19.30
Татаринов Е.Г.
(с октября)
Программирование Python. Профиль
10.00-12.00
Лантратов А.А.
8 класс
Олимпиадная физика
13.00-15.30
Лукьянов А.А. Олимпиадная математика
16.30-19.00
Порядин А.И.
9 класс
Профильная математика
(Подготовка к ОГЭ)
9.00-12.00
Котенко А.Е.
(с 14 октября)Информатика Python
(Подготовка к ОГЭ)
12.30-15.30
Лантратов А.А.Русский язык.
(Подготовка к ОГЭ)
17.00-20.00
Лочмелис Е.Р.
10 класс
Профильная математика
13.00-16.00
Порядин А.И. Экспресс-курс.
Профильная математика
12.30-15.30
Котенко А.Е.
(с 13 января)Экспресс-курс
"Русский язык.
ЕГЭ подготовка"
17.00-20.00
Алимов М.Р.
(с ноября)
11 класс
Профильная математика
Подготовка к ЕГЭ
13.00-16.00
Николаев Ю.П.
2 группа
(с октября)
Экспресс-курс
"Русский язык.
ЕГЭ подготовка"
17.00-20.00
Алимов М.Р.
(с ноября)
воскресенье
7 класс
Олимпиадная математика
16.00-18.00
Архарова М.Н.
8 класс
"Геометрия - это просто!" (Планиметрия)
12.00-14.30
Татаринов Е.Г.
(с октября)
9 класс
"Геометрия - это просто!" (Планиметрия)
12.00-14.30
Татаринов Е.Г.
(с октября)
10 класс
Русский язык.
(ЕГЭ подготовка)
17.00-20.00
Лочмелис Е.Р.
Набор закрыт
"Геометрия - это просто!" (Стереометрия)
17.00-20.00
Татаринов Е.Г.
(с октября)
11 класс
Русский язык.
(ЕГЭ подготовка)
17.00-20.00
Лочмелис Е.Р.
Набор закрытПрофильная физика ЕГЭ
10.00-13.00
Прохоров В.К.
Набор закрыт"Геометрия - это просто!" (Стереометрия)
17.00-20.00
Татаринов Е.Г.
(с октября)
Формат занятий
- г. Долгопрудный, Аудиторный корпус МФТИ
- г. Москва, Московский корпус МФТИ,
м. Новокузнецкая/ м. Третьяковская, ул. Климентовский пер. 1, стр. 1 - Онлайн занятия – на платформе zoom.
Тестирование
Тестирование проходит онлайн.
Стоимость курсов
|
Класс |
Кол-во ак.ч. за 1 занятие по выбранному курсу |
Предметы* |
Очно |
Онлайн |
Кол-во часов за 1 курс, руб |
Стоимость 1 полного курса по выбранному предмету, руб |
Количество занятий за 1 курс по выбранному предмету** |
|||
|
Стоимость 1 занятия по выбранному предмету, руб |
Стоимость за 4 занятия по выбранному предмету, руб |
Стоимость 1 занятия по выбранному предмету, руб |
Стоимость за 4 занятия по выбранному предмету, руб |
|||||||
|
Очно/онлайн |
||||||||||
|
7 класс |
2,5 |
«Профильная математика» |
1625 |
6500 |
1475 |
5900 |
90 |
58500/ 53100 |
36 |
|
|
«Олимпиадная математика |
||||||||||
|
«Профильная физика» |
||||||||||
|
«Олимпиадная физика» |
||||||||||
|
8 класс |
3 |
«Профильная математика» |
1800 |
7200 |
1675 |
6700 |
108 |
64800/60300 |
36 |
|
|
«Олимпиадная математика |
||||||||||
|
«Профильная физика» |
||||||||||
|
«Олимпиадная физика» |
||||||||||
|
9-11 классы |
4 |
«Профильная математика» (подготовка к ГИА) |
2025 |
8100 |
1900 |
7600 |
144 |
72900/68400 |
36 |
|
|
«Профильная физика» (Подготовка к ГИА) |
||||||||||
|
«Информатика» (Подготовка к ГИА) |
|
|||||||||
|
«Русский язык» (Подготовка к ГИА) |
|
|||||||||
|
7 - 8 класс |
2,5 |
Компьютерная физика (сентябрь-апрель) |
1625 |
6500 |
1475 |
5900 |
80 |
52000/47200 |
32 |
|
|
7 класс |
|
Программирование |
1625 |
6500 |
1475 |
5900 |
90 |
58500/ 53100 |
36 |
|
|
8-11 класс |
4 |
Программирование |
2025 |
8100 |
1900 |
7600 |
144 |
72900/68400 |
36 |
|
|
10 классы |
4 |
Математика. Подготовка к перечневым олимпиадам 2024 |
2300 |
9200 |
2150 |
8600 |
128*** |
73600/68800 |
32 |
|
|
Физика. Подготовка к перечневым олимпиадам 2024 |
|
|||||||||
|
Русский язык. Подготовка к перечневым олимпиадам 2024 |
|
|||||||||
|
11 классы |
4 |
Математика. Подготовка к перечневым олимпиадам 2024 |
2300 |
9200 |
2150 |
8600 |
88*** |
50600/47300 |
22 |
|
|
Физика. Подготовка к перечневым олимпиадам 2024 |
|
|||||||||
|
Русский язык. Подготовка к перечневым олимпиадам 2024 |
|
|||||||||
*Стоимость за месяц включает в себя 4 занятия, без привязки к календарному месяцу. Если в месяце 5 недель, значит пятая неделя переходит на другой месяц.
**Количество занятий за 1 курс рассчитано с учетом новогодних праздничных дней.
*** Занятия на курсах «Подготовка к перечневым олимпиадам 2024 (физика математика, русский язык) для 11 классов проходят с сентября по середину февраля (до заключительного этапа олимпиады). Группы 10 класса занимаются до конца апреля. После олимпиады на курсе происходит разбор ошибок.
Заключение договора
Договор заключается с родителями или с самим учащимся, достигшим 18 лет. При заключении договора потребуется:
паспорт лица, с которым заключается договор;
Договор необходимо предоставить не позднее 2 занятия, без договора учащиеся до занятий не допускаются.
Остались вопросы? Звоните!
8 (800) 302-77-42
8 (495) 542-65-62
8 (495) 743-29-02
Подготовительные курсы для школьников – это отличное решение для тех, кто хочет улучшить успеваемость, подготовиться к ЕГЭ, поступлению, к конкурсам или олимпиадам. Выбрав Подготовительные курсы МФТИ, вы можете быть уверены в высоком качестве образовательных услуг, заказать которые можно на выгодных условиях.
Ни для кого не секрет, что подготовка к Единым государственным экзаменам, олимпиадам и поступлению в ВУЗы вызывает массу переживаний у учащихся. Для того, что быть уверенным в собственных силах и знаниях, важно провести тщательную подготовку, восполнить имеющиеся пробелы и укрепить базу знаний.
Подготовительные курсы от МФТИ проходят по программам, утверждённым Учёным советом института. Посещая их, можно не только получить качественную и эффективную подготовку по различным дисциплинам, теоретическую базу и практические навыки, но и избавиться от страха и стать увереннее. Вашему вниманию представлены курсы для выпускников школ, младших школьников и старшеклассников, проводят которые ведущие специалисты с большим опытом.
Чтобы записаться на подготовительные курсы для школьников или задать любые дополнительные вопросы, звоните нам по телефону.
Курсы МФТИ онлайн
Если нет возможности очно посещать занятия по подготовке к ЕГЭ и поступлению, записывайте на курсы МФТИ онлайн. Зарегистрироваться на подготовительные курсы МФТИ можно прямо на сайте или по телефону.
Школьные уроки, занятия с репетитором, подготовки к олимпиадам у многих школьников занимают большую часть дня. Не всегда есть физическая возможность добавить в плотный распорядок дня еще одну поездку на аудиторные занятия. Онлайн-формат также удобен иногородним абитуриентам, которые выбрали для поступления хороший московский вуз, но не могут ездить на его подготовительные курсы 2-3 раза в неделю.
Занятия проходят в формате, который современным школьникам ближе. Достаточно иметь смартфон или ноутбук, чтобы прослушать очередную лекцию или пересмотреть для закрепления предыдущий материал. Кроме формата подачи материала, онлайн-курсы не отличаются от традиционных занятий в аудитории. Их проводят опытные преподаватели вуза. Для определения уровня подготовки и проверки знаний сдаются тестовые работы. Регулярные, вдумчивые занятия многократно повышают шансы на успешную сдачу ЕГЭ и облегчают поступление в вуз. Посещение подготовителкурсов МФТИ онлайн возможно после записи по телефону +7 (495) 542-65-62.